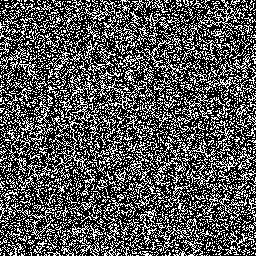Difference between revisions of "Pseudorandom number generators"
(→Blum Blum Shub) |
|||
| Line 181: | Line 181: | ||
# <math>q</math> random large prime | # <math>q</math> random large prime | ||
# <math>M</math> is th eproduct of <math>p</math> and <math>q</math> | # <math>M</math> is th eproduct of <math>p</math> and <math>q</math> | ||
| − | # <math>x_0</math> is the seed; usually an integer that is co-prime to <math>M</math><ref>Lenore Blum, Manuel Blum, and Michael Shub. "A Simple Unpredictable Pseudo-Random Number Generator", SIAM Journal on Computing, volume 15, pages 364–383, May 1986.</ref | + | # <math>x_0</math> is the seed; usually an integer that is co-prime to <math>M</math><ref>Lenore Blum, Manuel Blum, and Michael Shub. "A Simple Unpredictable Pseudo-Random Number Generator", SIAM Journal on Computing, volume 15, pages 364–383, May 1986.</ref> |
| Line 198: | Line 198: | ||
# [http://demonstrations.wolfram.com/MersenneTwisterAndFriends/ WolframAlpha - Mersenne Twister simulator] | # [http://demonstrations.wolfram.com/MersenneTwisterAndFriends/ WolframAlpha - Mersenne Twister simulator] | ||
# [http://cryptography.gmu.edu/~jkaps/download.php?docid=1083 Mersenne Twister – A Pseudo Random Number Generator and its Variants] | # [http://cryptography.gmu.edu/~jkaps/download.php?docid=1083 Mersenne Twister – A Pseudo Random Number Generator and its Variants] | ||
| − | |||
Revision as of 22:55, 6 December 2012
In cryptography, a pseudorandom generator (or PSG) is procedure that outputs a sequence computationally indistinguishable from truly random sequence with uniformly distributed random sequence. The prefix pseudo (from Greek ψευδής "lying, false") is used to mark something as false, fraudulent, or pretending to be something it is not. Pseudo random generators find application in many fields besides cryptography such as applied mathematics, physics and simulations. Simulations often require mechanisms producing sequences of random values. These procedures are certainly non-trivial and often require significant amounts of computational time.
Contents
Definition
A pseudorandom generator (or PRG) is a (deterministic) map Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{G:\{0, 1\}^l \rightarrow \{0, 1\}^n}}} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{n \geq l}}} . Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{l}}} is the 'seed length' and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{n - l \geq 0}}} is the 'stretch'. We typically think that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{n \gg l}}} and that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{G}}} is effciently computable in some model. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f:\{0, 1\}^n \rightarrow \{0, 1\}}}} is any 'statistical test', we say that G 'Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\epsilon}}} -fools' Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f}}} is
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{|Pr[f({U_n} = 1)] - Pr[f(G({U_l})) = 1)]| \leq \epsilon}}}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {U_m}}
denotes a uniformly random string in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\{0, 1\}^m}}}
. Here the string Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{U_l}}}
is called the 'seed'. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{C}}}
is a class of tests, we say that G 'Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\epsilon}}}
-fools Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{C}}}
' or is an 'Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\epsilon}}}
-PRG against Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{C}}}
' if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{G}}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\epsilon}}}
-fools Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f}}}
for every Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f \in C}}}
.[1]
In other words we are thying to convince any outside party (let's call them an adversary) that sequences returned from PRG are being produced chosen at random. Adversary may use statistical test algorithms to check simultaneously outputs from PRG and uniformly random sequnces. PRGs ensure that to the adversary both outputs look the same.
Required properties
Reliable PRG should have all these properties[2]:
- Unbiased - Uniform distribution
- All values of whatever samplesize is collected are equiprobable
- Unpredictable - Indipendence
- It is impossible to predict what the next output will be, given all the previous outputs, but not the internal state
- Unreproducible
- Two of the same generators, given the same starting conditions, will produce different outputs
- Long period
- The generator should be of long period
- Fast computation
- The generator should be reasonably fast
- Security
- The generator should be secured
Construction of simple PRG
There are many ways how to construct PRGs and one of the simpliest ones is to use pseudorandom functions and expand the key. A pseudorandom function (or PRF) is any function defined over Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal(K, X, Y)}}} :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{F:K \times X \rightarrow Y}}}
where:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{K}}} is key space
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{X}}} is input space
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{Y}}} is output space
such that exists efficient algorithm to evaluate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal F(k,x)}}} .[3]
On the other hand pseudorandom permutation is any function defined over Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal(K, X)}}}
:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{E:K \times X \rightarrow X}}}
such that[3]:
- Exists efficient deterministic algorithm to evaluate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal E(k,x)}}}
- The function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal F(k,\cdot)}}} is one-to-one
- Exists efficient inversion algorithm Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal D(k,y)}}}
Any pseudorandom permutation (or PRP) is also pseudorandom function given
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{X=Y}}}
- Function is efficiently invertible
So let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{F: K \times \{0, 1\}^n \rightarrow \{0, 1\}^n}}}
be a PRF
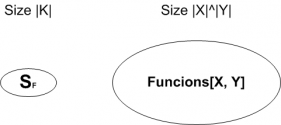
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{ \begin{cases} Functions[X, Y]: \text{ all functions from X to Y}\\ S_F = {F(k, \cdot) st. k \in K} \subseteq Functions[X, Y] \end{cases} }
For PRF to be suitable for use in PRG it must be secure and therefore computationally indistinguishable from random function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f(\cdot)}}}
. This situation is depicted below:
The adversary can not distinguish whether output came from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{S_F}}}
or some random Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f(\cdot)}}}
.
If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{F}}}
is secure PRF we can use key expantion to construct secure PRG defined as
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{G: K \times \{0, 1\}^{nt}}}}
where:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{n}}} number of bits in each block
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{t}}} number of generated blocks
We get return value by using key expansion. Great advantage of using this approach is ability to employ multiple CPU cores and take advantage of paralelization (for example odd values are computed by core 1; even values are computed by core 2). Security of PRG is provided by fact that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{F(k, \cdot)}}}
is indistinguishable form random Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f(\cdot)}}}
.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{G(k) = F(k, 0) || F(k, 1) || ... || F(k, t-1)}}}
Linear methods
Linear Congruent Generator
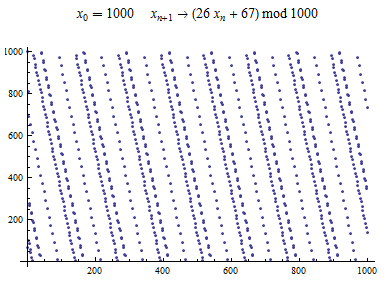
Linear Congruent Generator (or LCG) is one of the best known PRGs in the world. This generator is defined as follows
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X_{n+1} \equiv \left( a X_n + c \right)~~\pmod{m}}
where:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X_{n}} is the sequence of pseudorandom values
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X_0,\,0 \le X_0 < m} is the seed
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a,\,0 < a < m} is the multiplier
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle c,\,0 \le c < m} is the increment
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle m,\, 0<m } is the modulo
are integer constants that specify the generator.[4]
The range of output values is restricted since after at most Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle m} values the period starts to repeat itself (in the terms of repeating the same pattern). The most significant element in terms of the length of the period is the multiplier. Best outputs from generator in regard of the length of the period are provided given values:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a - 1} is divisable by all the primes that divide the multiplier
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a - 1} is multiple of number 4, when the multiplier is multiple of number 4
- the multiplier and the increment do not have common divisor (except from 1)
An example of output exported from WolframAplha application[5]:
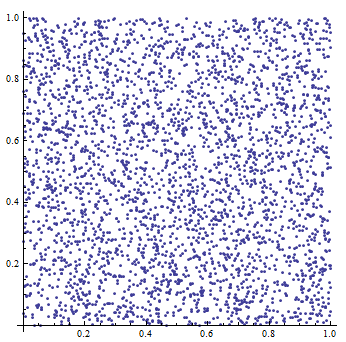
Multiplicative Congruent Generator
Multiplicative Congruent Generator (or MCG) is simplyfied version of LCG since if c = 0 in LCG we get the MCG[4]. This generator is defined as follows:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X_{n+1} \equiv a X_n ~~\pmod{m}}
where:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X_{n}} is the sequence of pseudorandom values
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X_0,\,0 \le X_0 < m} is the seed
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a,\,0 < a < m} is the multiplier
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle m,\, 0<m } is the modulo
An example of output (of 59-bit multiplicative congruential generator) exported from WolframAplha application[6]:
Lagged Fibonacci generator
Lagged Fibonacci generator (or LFG) is one of the fastest PRGs and they provide long periods. LFG is defined as follows
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle LFG(p, q, \bigoplus)}
where:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} is coeficient of lag, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p > q}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q} is coeficient of lag, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p > q}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \bigoplus} binary operation such as adding or subtracting in modulo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle m} , multiplication in modulo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle m} or bitwise exclusive Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle OR} (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle XOR} )
and the sequence is defined by
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_n = x_{n-p} \bigoplus x_{n-q}}
For generator to work, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q}
must be odd numbers. Generator stores used Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p}
values in a lag table. In order to achieve the maximum length of the period and fair degree of randomness parameters need to be set in the following way:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle m = 2^b}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q} have values of powers of primitive polynomials
producing the length of the period for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle XOR} :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P = 2^p - 1} [7]
An example of an output[8]:
Mersenne twister
Mersenne twister (or MT) is one of the modern implementations of PRGs and it provides very high quality of peudorandom numbers. It was developed by Makoto Matsumoto and Takuji Nishimura in 1997 with aim to replace some known faults of older PRGs. MT is founded on a matrix linear recurrence over a finite binary field. Nowadays, the most used versions are MT with 32 and 64 bit word length. Due to optimizations applied to MT it is optimized to be used in Monte Carlo method simulaions in many fields of science.
Since the description of algorithm is quite , I would like to point the readers to this paper from George Mason University where the internal mechanics of MT are explained in detail.
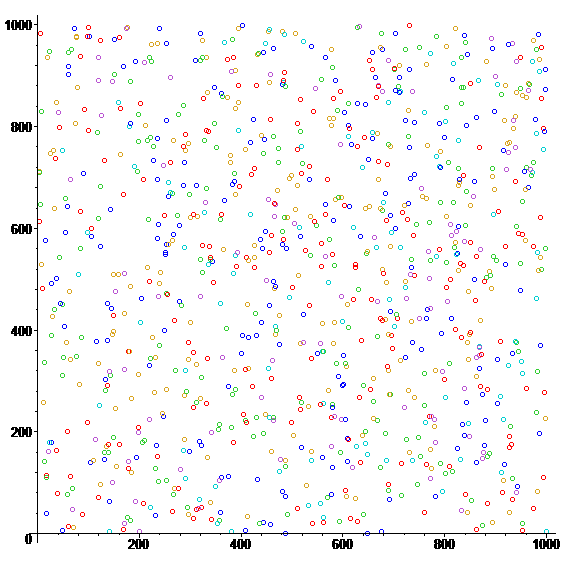
An example of output (of Mersenne twister shift register generator) exported from WolframAplha application[6]:
Nonlinear methods
Blum Blum Shub
Blum Blum Shub (or BBS) is PRG developed by Lenore Blum, Manuel Blum and Michael Shub in 1986. It is defined as follows:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_{n+1} = x_n^2 \hspace{0.5cm} mod M}
where:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} random large prime
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q} random large prime
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M} is th eproduct of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_0} is the seed; usually an integer that is co-prime to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M} [9]
BBS does not find application in simulations due to its running time. On the other hand due to it's security properties it is appropriate for use in cryptography.
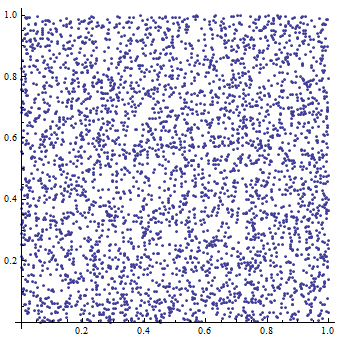
An example of output constructed in Maple 14 (seed=10, range=1000):
Testing
<TODO>
References
- ↑ Lecture 16: Nisan's PRG for small space, 15-855: Intensive Intro to Complexity Theory. Spring 2009, Carnegie Mellon University, USA.: page 1
- ↑ Xiang-Yang Li, Pseudo-random Number - Cryptography and Network Security. Illinois Institute of Technology, USA
- ↑ 3.0 3.1 Boneh, D. (2012); Lecture 3 - Block ciphers, Introduction to Cryptography. Stanford, USA.
- ↑ 4.0 4.1 Knuth 1997, Sec. 3.2.1
- ↑ WolframAlpha - Linear Congruential Generators (2012)
- ↑ 6.0 6.1 WolframAlpha - Mersenne Twister and Friends (2012)
- ↑ Mikulka Z., (2008); Random Number Generators - Bachelor’s thesis. University of technology - Faculty of electrical engeneering and communication, Department of telecomunications, Brno.: page 14
- ↑ SPRNG Libraries Documentation
- ↑ Lenore Blum, Manuel Blum, and Michael Shub. "A Simple Unpredictable Pseudo-Random Number Generator", SIAM Journal on Computing, volume 15, pages 364–383, May 1986.