Difference between revisions of "Pseudorandom number generators"
(Blanked the page) |
|||
| Line 1: | Line 1: | ||
| + | In cryptography, a pseudorandom generator (or PSG) is procedure that outputs a sequence computationally indistinguishable from truly random sequence with uniformly distributed random sequence. The prefix pseudo (from Greek ?????? "lying, false") is used to mark something as false, fraudulent, or pretending to be something it is not. Pseudo random generators find application in many fields besides cryptography such as applied mathematics, physics and simulations. | ||
| + | Simulations often require mechanisms producing sequences of random values. These procedures are certainly non-trivial and often require significant amounts of computational time. | ||
| + | |||
| + | __TOC__ | ||
| + | |||
| + | == Definition == | ||
| + | A pseudorandom generator (or PRG) is a (deterministic) map <math>{{G:\{0, 1\}^l \rightarrow \{0, 1\}^n}}</math>, where <math>{{n \geq l}}</math>. Here <math>{{l}}</math> is the 'seed length' and <math>{{n - l \geq 0}}</math> is the 'stretch'. We typically think that <math>{{n \gg l}}</math> and that <math>{{G}}</math> is effciently computable in some model. If <math>{{f:\{0, 1\}^n \rightarrow \{0, 1\}}}</math> is any 'statistical test', we say that G '<math>{{\epsilon}}</math>-fools' <math>{{f}}</math> is | ||
| + | |||
| + | |||
| + | <math>{{|Pr[f({U_n} = 1)] - Pr[f(G({U_l})) = 1)]| \leq \epsilon}}</math> | ||
| + | |||
| + | |||
| + | where <math>{U_m}</math> denotes a uniformly random string in <math>{{\{0, 1\}^m}}</math>. Here the string <math>{{U_l}}</math> is called the 'seed'. If <math>{{C}}</math> is a class of tests, we say that G '<math>{{\epsilon}}</math>-fools <math>{{C}}</math>' or is an '<math>{{\epsilon}}</math>-PRG against <math>{{C}}</math>' if <math>{{G}}</math> <math>{{\epsilon}}</math>-fools <math>{{f}}</math> for every <math>{{f \in C}}</math>.<ref name="cmu">[http://www.cs.cmu.edu/~odonnell/complexity/docs/lecture16.pdf Lecture 16: Nisan's PRG for small space, 15-855: Intensive Intro to Complexity Theory. Spring 2009, Carnegie Mellon University, USA.]: page 1</ref> | ||
| + | |||
| + | |||
| + | In other words we are thying to convince any outside party (let's call them an adversary) that sequences returned from PRG are being produced chosen at random. Adversary may use statistical test algorithms to check simultaneously outputs from PRG and uniformly random sequnces. PRGs ensure that to the adversary both outputs look the same. | ||
| + | |||
| + | == Required properties == | ||
| + | Reliable PRG should have all these properties<ref name="props">[http://www.cs.iit.edu/~cs549/lectures/CNS-6-2-handout.pdf Xiang-Yang Li, Pseudo-random Number - Cryptography and Network Security. Illinois Institute of Technology, USA]</ref>: | ||
| + | * Unbiased - Uniform distribution | ||
| + | ** All values of whatever samplesize is collected are equiprobable | ||
| + | * Unpredictable - Indipendence | ||
| + | ** It is impossible to predict what the next output will be, given all the previous outputs, but not the internal state | ||
| + | * Unreproducible | ||
| + | ** Two of the same generators, given the same starting conditions, will produce different outputs | ||
| + | * Long period | ||
| + | ** The generator should be of long period | ||
| + | * Fast computation | ||
| + | ** The generator should be reasonably fast | ||
| + | * Security | ||
| + | ** The generator should be secured | ||
| + | |||
| + | == Construction of simple PRG == | ||
| + | There are many ways how to construct PRGs and one of the simpliest ones is to use pseudorandom functions and expand the key. A pseudorandom function (or PRF) is any function defined over <math>{{\textnormal(K, X, Y)}}</math> : | ||
| + | |||
| + | <math>{{F:K \times X \rightarrow Y}}</math> | ||
| + | |||
| + | where: | ||
| + | |||
| + | # <math>{{K}}</math> is key space | ||
| + | # <math>{{X}}</math> is input space | ||
| + | # <math>{{Y}}</math> is output space | ||
| + | |||
| + | such that exists efficient algorithm to evaluate <math>{{\textnormal F(k,x)}}</math>.<ref name=crypto>[https://class.coursera.org/crypto/class/index Boneh, D. (2012); Lecture 3 - Block ciphers, Introduction to Cryptography. Stanford, USA.]</ref> | ||
| + | |||
| + | |||
| + | On the other hand pseudorandom permutation is any function defined over <math>{{\textnormal(K, X)}}</math>: | ||
| + | |||
| + | <math>{{E:K \times X \rightarrow X}}</math> | ||
| + | |||
| + | such that<ref name=crypto/>: | ||
| + | |||
| + | # Exists efficient deterministic algorithm to evaluate <math>{{\textnormal E(k,x)}}</math> | ||
| + | # The function <math>{{\textnormal F(k,\cdot)}}</math> is one-to-one | ||
| + | # Exists efficient inversion algorithm <math>{{\textnormal D(k,y)}}</math> | ||
| + | |||
| + | |||
| + | Any pseudorandom permutation (or PRP) is also pseudorandom function given | ||
| + | # <math>{{X=Y}}</math> | ||
| + | # Function is efficiently invertible | ||
| + | |||
| + | |||
| + | So let <math>{{F: K \times \{0, 1\}^n \rightarrow \{0, 1\}^n}}</math> be a PRF | ||
| + | |||
| + | |||
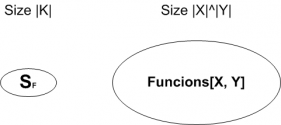
| + | <math>{{ | ||
| + | \begin{cases} | ||
| + | Functions[X, Y]: \text{ all functions from X to Y}\\ | ||
| + | S_F = {F(k, \cdot) st. k \in K} \subseteq Functions[X, Y] | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | For PRF to be suitable for use in PRG it must be secure and therefore computationally indistinguishable from random function <math>{{f(\cdot)}}</math>. This situation is depicted below: | ||
| + | |||
| + | |||
| + | [[File:secure_prf.png|x125px]] | ||
| + | |||
| + | |||
| + | The adversary can not distinguish whether output came from <math>{{S_F}}</math> or some random <math>{{f(\cdot)}}</math>. | ||
| + | |||
| + | |||
| + | If <math>{{F}}</math> is secure PRF we can use key expantion to construct secure PRG defined as | ||
| + | |||
| + | |||
| + | <math>{{G: K \times \{0, 1\}^{nt}}}</math> | ||
| + | where: | ||
| + | # <math>{{n}}</math> number of bits in each block | ||
| + | # <math>{{t}}</math> number of generated blocks | ||
| + | |||
| + | |||
| + | We get return value by using key expansion. Great advantage of using this approach is ability to employ multiple CPU cores and take advantage of paralelization (for example odd values are computed by core 1; even values are computed by core 2). Security of PRG is provided by fact that <math>{{F(k, \cdot)}}</math> is indistinguishable form random <math>{{f(\cdot)}}</math>. | ||
| + | |||
| + | <math>{{G(k) = F(k, 0) || F(k, 1) || ... || F(k, t-1)}}</math> | ||
| + | |||
| + | |||
| + | |||
| + | ==References== | ||
| + | <references /> | ||
Revision as of 23:46, 1 December 2012
In cryptography, a pseudorandom generator (or PSG) is procedure that outputs a sequence computationally indistinguishable from truly random sequence with uniformly distributed random sequence. The prefix pseudo (from Greek ?????? "lying, false") is used to mark something as false, fraudulent, or pretending to be something it is not. Pseudo random generators find application in many fields besides cryptography such as applied mathematics, physics and simulations. Simulations often require mechanisms producing sequences of random values. These procedures are certainly non-trivial and often require significant amounts of computational time.
Definition
A pseudorandom generator (or PRG) is a (deterministic) map Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{G:\{0, 1\}^l \rightarrow \{0, 1\}^n}}} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{n \geq l}}} . Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{l}}} is the 'seed length' and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{n - l \geq 0}}} is the 'stretch'. We typically think that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{n \gg l}}} and that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{G}}} is effciently computable in some model. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f:\{0, 1\}^n \rightarrow \{0, 1\}}}} is any 'statistical test', we say that G 'Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\epsilon}}} -fools' Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f}}} is
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{|Pr[f({U_n} = 1)] - Pr[f(G({U_l})) = 1)]| \leq \epsilon}}}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {U_m}}
denotes a uniformly random string in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\{0, 1\}^m}}}
. Here the string Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{U_l}}}
is called the 'seed'. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{C}}}
is a class of tests, we say that G 'Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\epsilon}}}
-fools Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{C}}}
' or is an 'Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\epsilon}}}
-PRG against Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{C}}}
' if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{G}}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\epsilon}}}
-fools Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f}}}
for every Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f \in C}}}
.[1]
In other words we are thying to convince any outside party (let's call them an adversary) that sequences returned from PRG are being produced chosen at random. Adversary may use statistical test algorithms to check simultaneously outputs from PRG and uniformly random sequnces. PRGs ensure that to the adversary both outputs look the same.
Required properties
Reliable PRG should have all these properties[2]:
- Unbiased - Uniform distribution
- All values of whatever samplesize is collected are equiprobable
- Unpredictable - Indipendence
- It is impossible to predict what the next output will be, given all the previous outputs, but not the internal state
- Unreproducible
- Two of the same generators, given the same starting conditions, will produce different outputs
- Long period
- The generator should be of long period
- Fast computation
- The generator should be reasonably fast
- Security
- The generator should be secured
Construction of simple PRG
There are many ways how to construct PRGs and one of the simpliest ones is to use pseudorandom functions and expand the key. A pseudorandom function (or PRF) is any function defined over Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal(K, X, Y)}}} :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{F:K \times X \rightarrow Y}}}
where:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{K}}} is key space
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{X}}} is input space
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{Y}}} is output space
such that exists efficient algorithm to evaluate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal F(k,x)}}} .[3]
On the other hand pseudorandom permutation is any function defined over Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal(K, X)}}}
:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{E:K \times X \rightarrow X}}}
such that[3]:
- Exists efficient deterministic algorithm to evaluate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal E(k,x)}}}
- The function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal F(k,\cdot)}}} is one-to-one
- Exists efficient inversion algorithm Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal D(k,y)}}}
Any pseudorandom permutation (or PRP) is also pseudorandom function given
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{X=Y}}}
- Function is efficiently invertible
So let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{F: K \times \{0, 1\}^n \rightarrow \{0, 1\}^n}}}
be a PRF
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{ \begin{cases} Functions[X, Y]: \text{ all functions from X to Y}\\ S_F = {F(k, \cdot) st. k \in K} \subseteq Functions[X, Y] \end{cases} }
For PRF to be suitable for use in PRG it must be secure and therefore computationally indistinguishable from random function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f(\cdot)}}}
. This situation is depicted below:
The adversary can not distinguish whether output came from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{S_F}}}
or some random Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f(\cdot)}}}
.
If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{F}}}
is secure PRF we can use key expantion to construct secure PRG defined as
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{G: K \times \{0, 1\}^{nt}}}}
where:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{n}}} number of bits in each block
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{t}}} number of generated blocks
We get return value by using key expansion. Great advantage of using this approach is ability to employ multiple CPU cores and take advantage of paralelization (for example odd values are computed by core 1; even values are computed by core 2). Security of PRG is provided by fact that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{F(k, \cdot)}}}
is indistinguishable form random Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{f(\cdot)}}}
.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{G(k) = F(k, 0) || F(k, 1) || ... || F(k, t-1)}}}
References
- ↑ Lecture 16: Nisan's PRG for small space, 15-855: Intensive Intro to Complexity Theory. Spring 2009, Carnegie Mellon University, USA.: page 1
- ↑ Xiang-Yang Li, Pseudo-random Number - Cryptography and Network Security. Illinois Institute of Technology, USA
- ↑ 3.0 3.1 Boneh, D. (2012); Lecture 3 - Block ciphers, Introduction to Cryptography. Stanford, USA.