Difference between revisions of "Pseudorandom number generators"
(→Definition) |
(→Definition) |
||
| Line 11: | Line 11: | ||
<math>{{E:K \times X \rightarrow Y}}</math> | <math>{{E:K \times X \rightarrow Y}}</math> | ||
| − | such that exists efficient algorithm to evaluate <math>{{\textnormal F(k,x)}}</math>. | + | such that exists efficient algorithm to evaluate <math>{{\textnormal F(k,x)}}</math>.<ref name="crypto">Dan Boneh, Stanford - Introduction to Cryptography, Lecture 3 - Block ciphers</ref> |
Revision as of 15:47, 1 December 2012
In cryptography, a pseudorandom generator (or PSG) is procedure that outputs a sequence computationally indistinguishable from truly random sequence with uniformly distributed random sequence. The prefix pseudo (from Greek ψευδής "lying, false") is used to mark something as false, fraudulent, or pretending to be something it is not. Pseudo random generators find application in many fields besides cryptography such as applied mathematics, physics and simulations. Simulations often require mechanisms producing sequences of random values. These procedures are certainly non-trivial and often require significant amounts of computational time.
Contents
Definition
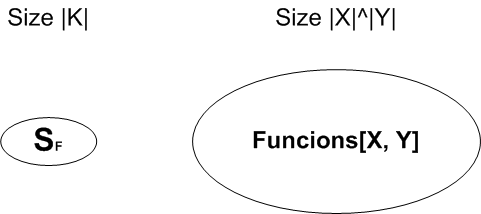
First of all let’s start with pseudorandom functions. A pseudorandom function is any function defined over Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal(K, X, Y)}}} :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{E:K \times X \rightarrow Y}}}
such that exists efficient algorithm to evaluate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal F(k,x)}}} .[1]
On the other hand pseudorandom permutation is any function defined over Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal(K, X)}}}
:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{E:K \times X \rightarrow X}}}
such that:
- Exists efficient deterministic algorithm to evaluate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal E(k,x)}}}
- The function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal F(k,\cdot)}}} is one-to-one
- Exists efficient inversion algorithm Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {{\textnormal D(k,y)}}}
- ↑ Dan Boneh, Stanford - Introduction to Cryptography, Lecture 3 - Block ciphers