Difference between revisions of "System Dynamics/cs"
| (34 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
[[File:zebry_system.png|thumb|right|400 px|Příklad chování systému]] | [[File:zebry_system.png|thumb|right|400 px|Příklad chování systému]] | ||
| − | '''Systémová dynamika''' je prakticky orientovaná disciplína pro studium chování komplexních sociálních systémů, která zdůrazňuje vztah mezi strukturou těchto systémů a výsledným chováním. Systémová dynamika se snaží objevovat v komplexních systémech určité '''vzory chování''', které je možno zobecnit do podoby tzv. archetypů. Tyto vzorce chování jsou modelovány pomocí '''systému vnitřních smyček, zpětných vazeb a časových prodlev'''. Mezi hlavní přínosy této vědní disciplíny je možné zařadit schopnost modelovat skutečný svět, schopnost pojmout složitosti a vazby na zpětné struktury, které jsou v těchto sociálních systémech; nezbytné je také využití počítačových modelů a simulací – jádrem systémové dynamiky je vytváření explicitních modelů. | + | '''Systémová dynamika''' je prakticky orientovaná disciplína pro studium chování komplexních sociálních systémů, která zdůrazňuje vztah mezi strukturou těchto systémů a výsledným chováním. Systémová dynamika se snaží objevovat v komplexních systémech určité '''vzory chování''', které je možno zobecnit do podoby tzv. archetypů. Tyto vzorce chování jsou modelovány pomocí '''systému vnitřních smyček, zpětných vazeb a časových prodlev'''. Mezi hlavní přínosy této vědní disciplíny je možné zařadit schopnost modelovat skutečný svět, schopnost pojmout složitosti a vazby na zpětné struktury, které jsou v těchto sociálních systémech; nezbytné je také využití počítačových modelů a simulací – jádrem systémové dynamiky je vytváření explicitních modelů.<ref name="systémová dynamika">MILDEOVÁ, Stanislava a Viktor VOJTKO, 2003. Systémová dynamika. V Praze: Oeconomica. ISBN 80-245-0626-2. |
| + | </ref> | ||
| − | Vznik systémové dynamiky je spojován s řešením reálné situace, která nastala ve firmě General Electrics v 50. letech 20. století – společnost nemohla vyřešit stále opakující se problém, kdy dělníci museli v jednom roce pracovat na tři, nebo čtyři směny a v dalším roce bylo nutné polovinu dělníků propustit. Vedení společnosti přisuzovalo tyto výkyvy změnám v ekonomickém cyklu a v poptávce, nicméně pomocí počítačových simulací zjistili, že vztah mezi objednávkami, skladovými zásobami a zaměstnaností spočívá ve vnitřní determinovanosti systému, tedy politikách, podle kterých se rozhodovalo – celý systém byl ovlivněn faktory, které vedení společnosti vůbec původně nevzalo v potaz. | + | Vznik systémové dynamiky je spojován s řešením reálné situace, která nastala ve firmě General Electrics v 50. letech 20. století – společnost nemohla vyřešit stále opakující se problém, kdy dělníci museli v jednom roce pracovat na tři, nebo čtyři směny a v dalším roce bylo nutné polovinu dělníků propustit. Vedení společnosti přisuzovalo tyto výkyvy změnám v ekonomickém cyklu a v poptávce, nicméně pomocí počítačových simulací zjistili, že vztah mezi objednávkami, skladovými zásobami a zaměstnaností spočívá ve vnitřní determinovanosti systému, tedy politikách, podle kterých se rozhodovalo – celý systém byl ovlivněn faktory, které vedení společnosti vůbec původně nevzalo v potaz. <ref name="systémová dynamika">MILDEOVÁ, Stanislava a Viktor VOJTKO, 2003. Systémová dynamika. V Praze: Oeconomica. ISBN 80-245-0626-2. |
| + | </ref> | ||
| − | '''K podobným reakcím dochází v komplexních systémech neustále''' – Spojené státy americké celoročně vydají na zdravotní péči více než jakákoli jiná země na světě (v absolutní výši i poměrně k HDP), ale i přesto více než 40 milionů obyvatel nemá zdravotní pojištění, a Spojeným státům zároveň patří spodní příčky mezi vyspělými zeměmi z hlediska průměrné délky života a kojenecké úmrtnosti; komplexní výstavby nových dálnic za účelem snížení hustoty dopravy ve špičkách naopak dopravu ztěžují a zhoršují znečištění a kvalitu životního prostředí; antibiotika a nové léky urychlily evoluci rezistentních bakterií a patogenů, agresivní pesticidy a herbicidy podpořily vývoj odolných odrůd plevele a hmyzu, vyhubily přirozené predátory a často stojí za otravou ryb, ptáků a jiných živočichů. Toto zdánlivé paradoxní chování systémů je cílem zkoumání systémové dynamiky. | + | '''K podobným reakcím dochází v komplexních systémech neustále''' – Spojené státy americké celoročně vydají na zdravotní péči více než jakákoli jiná země na světě (v absolutní výši i poměrně k HDP), ale i přesto více než 40 milionů obyvatel nemá zdravotní pojištění, a Spojeným státům zároveň patří spodní příčky mezi vyspělými zeměmi z hlediska průměrné délky života a kojenecké úmrtnosti; komplexní výstavby nových dálnic za účelem snížení hustoty dopravy ve špičkách naopak dopravu ztěžují a zhoršují znečištění a kvalitu životního prostředí; antibiotika a nové léky urychlily evoluci rezistentních bakterií a patogenů, agresivní pesticidy a herbicidy podpořily vývoj odolných odrůd plevele a hmyzu, vyhubily přirozené predátory a často stojí za otravou ryb, ptáků a jiných živočichů. Toto zdánlivé paradoxní chování systémů je cílem zkoumání systémové dynamiky. <ref name="system dynamics model">[http://www.systemdynamics.org/conferences/2002/proceed/papers/CAREVIEW/C2STERMA.PDF STERMAN, John, 2001. System Dynamics Modeling: TOOLS FOR LEARNING IN A COMPLEX WORLD. University of California.] </ref> |
=Historie systémové dynamiky= | =Historie systémové dynamiky= | ||
| Line 26: | Line 28: | ||
Systémová (původně průmyslová) dynamika byla založena profesorem '''J. W. Forresterem''' ze Sloan School of Management na Massachusetts Institute of Technology. První článek týkající se této nové vědní disciplíny byl publikován v roce 1958, později využit jako druhá kapitola knihy od téhož autora „Industrial Dynamics“ z roku 1961. Na konci 50. let byl vyvinut první formální počítačový jazyk pro tvorbu modelů a simulací SIMPLE (Simulation of Industrial Management Probems with Lots of Equations), jehož autorem je Richard Bennett. | Systémová (původně průmyslová) dynamika byla založena profesorem '''J. W. Forresterem''' ze Sloan School of Management na Massachusetts Institute of Technology. První článek týkající se této nové vědní disciplíny byl publikován v roce 1958, později využit jako druhá kapitola knihy od téhož autora „Industrial Dynamics“ z roku 1961. Na konci 50. let byl vyvinut první formální počítačový jazyk pro tvorbu modelů a simulací SIMPLE (Simulation of Industrial Management Probems with Lots of Equations), jehož autorem je Richard Bennett. | ||
| − | Až do konce 60. let 20. století byla Systémová dynamika aplikována téměř výhradně na řešení manažerských problémů (60. léta byla charakteristická stagnací či bankrotem velkého množství technologických firem, které zprvu velmi rychle rostly – na základě tohoto fenoménu vznikl jeden ze základních systémových archetypů, model mezí růstu (Limits to Growth)). | + | Až do konce 60. let 20. století byla Systémová dynamika aplikována téměř výhradně na řešení manažerských problémů (60. léta byla charakteristická stagnací či bankrotem velkého množství technologických firem, které zprvu velmi rychle rostly – na základě tohoto fenoménu vznikl jeden ze základních systémových archetypů, model [http://www.simulace.info/index.php/Limits_to_Growth/cs mezí růstu (Limits to Growth)]). <ref name="ambroz">AMBROŽ, Ondřej, 2015. Systémová dynamika v projektech řízení kvality. Praha. Diplomová práce. Vysoká škola ekonomická v Praze.</ref> |
| + | [[File:58.jpg|thumb|left|200 px|publikace Urban Dynamics od J.W.Forrestera]] | ||
V roce 1968 se Systémová dynamika rozšířila díky spolupráci J. Forrestera a Johna Collinse, bývalého starosty Bostonu, i do oblasti '''urbanistiky a urbanistického rozvoje'''. Tato část vědy se zabývala zjištěním příčin toho, proč vznikají ve městech oblasti s vysokou mírou kriminality. Kniha Urban Dynamics, která vzešla z analýzy těchto poznatků, vedla právě ke zjištění, že některé základní politiky na zlepšení životní úrovně obyvatelstva jsou kontraproduktivní a byla ve své době považována téměř za kontroverzní dílo. | V roce 1968 se Systémová dynamika rozšířila díky spolupráci J. Forrestera a Johna Collinse, bývalého starosty Bostonu, i do oblasti '''urbanistiky a urbanistického rozvoje'''. Tato část vědy se zabývala zjištěním příčin toho, proč vznikají ve městech oblasti s vysokou mírou kriminality. Kniha Urban Dynamics, která vzešla z analýzy těchto poznatků, vedla právě ke zjištění, že některé základní politiky na zlepšení životní úrovně obyvatelstva jsou kontraproduktivní a byla ve své době považována téměř za kontroverzní dílo. | ||
| − | S postupným rozvojem počítačů a systémových modelů docházelo k rozvoji nástrojů pro dynamické modelování – simulační jazyk DYNAMO, simulační software Vensim, Powersim a STELLA; od 70. let bylo systematické modelování zejména v USA značně rozšířeno, a to i například na oblast projektového managementu. | + | |
| + | S postupným rozvojem počítačů a systémových modelů docházelo k rozvoji nástrojů pro dynamické modelování – simulační jazyk DYNAMO, simulační software Vensim, Powersim a STELLA; od 70. let bylo systematické modelování zejména v USA značně rozšířeno, a to i například na oblast projektového managementu.<ref name="ambroz">AMBROŽ, Ondřej, 2015. Systémová dynamika v projektech řízení kvality. Praha. Diplomová práce. Vysoká škola ekonomická v Praze.</ref> | ||
V '''České republice''' se využití systémové dynamiky rozvíjelo od 70. let zejména v univerzitním prostředí, poté až od roku 1995 i v komerčních sférách a státním sektoru; dynamické modelování bylo využito např. pro podporu plánování v Českém Telecomu, pro Armádu ČR byl vytvořen personalistický model, který obsahoval mj. demografii, trh pracovních sil a mobilitu pracovních sil. | V '''České republice''' se využití systémové dynamiky rozvíjelo od 70. let zejména v univerzitním prostředí, poté až od roku 1995 i v komerčních sférách a státním sektoru; dynamické modelování bylo využito např. pro podporu plánování v Českém Telecomu, pro Armádu ČR byl vytvořen personalistický model, který obsahoval mj. demografii, trh pracovních sil a mobilitu pracovních sil. | ||
| − | Ve všech výše uvedených příkladech byly modely použity pro získání prvotního vhledu do problematiky – poznání endogenní smyčkové zpětnovazební struktury příčin a následků, která vede k problémovému chování komplexního systému. Na základě těchto informací bylo možné ověřit logické důsledky a dopad rozhodnutí na celý systém. | + | Ve všech výše uvedených příkladech byly modely použity pro získání prvotního vhledu do problematiky – poznání endogenní smyčkové zpětnovazební struktury příčin a následků, která vede k problémovému chování komplexního systému. Na základě těchto informací bylo možné ověřit logické důsledky a dopad rozhodnutí na celý systém.<ref name="systémová dynamika">MILDEOVÁ, Stanislava a Viktor VOJTKO, 2003. Systémová dynamika. V Praze: Oeconomica. ISBN 80-245-0626-2. |
| + | </ref> | ||
| + | |||
| + | |||
=Základní koncepty systémové dynamiky= | =Základní koncepty systémové dynamiky= | ||
| − | ===Komplexní systémy=== | + | ===Komplexní systémy<ref name="systémová dynamika">MILDEOVÁ, Stanislava a Viktor VOJTKO, 2003. Systémová dynamika. V Praze: Oeconomica. ISBN 80-245-0626-2.</ref>=== |
| − | Před vlastním vymezením oblasti zájmu systémové dynamiky je nutné pochopit, kterými systémy se zabývá; komplexní systém představuje uskupení vzájemně propojených a ovlivňujících se prvků, které tvoří celek a má následující základní charakteristiky: | + | Před vlastním vymezením oblasti zájmu systémové dynamiky je nutné pochopit, kterými systémy se zabývá; komplexní systém představuje uskupení vzájemně propojených a ovlivňujících se prvků, které tvoří celek a má následující základní charakteristiky<ref name="kirkwood">[http://www.public.asu.edu/~kirkwood/sysdyn/SDIntro/preface.pdf KIRKWOOD, Craig, 1998. System Dynamics Methods: A quick introduction. Arizona State University.]</ref>: |
*'''Vzájemná závislost''' (interdipendence) – čím více jsou na sobě prvky závislé, tím méně je možné pochopit chování systému pouze na základě pochopení jednotlivých prvků. | *'''Vzájemná závislost''' (interdipendence) – čím více jsou na sobě prvky závislé, tím méně je možné pochopit chování systému pouze na základě pochopení jednotlivých prvků. | ||
| Line 51: | Line 58: | ||
===Zpětná vazba=== | ===Zpětná vazba=== | ||
| − | Složité systémy fungují jako celek; jejich chování je řízeno cyklickým vzorcem informací, kterému říkáme '''zpětnovazební smyčka'''. V praxi to znamená, že jedna část systému ovlivňuje systém jako celek a systém může zpětně onu část ovlivňovat a vzniká tak nová kvalita. Příkladem může být jízda na kole – rovnovážný aparát člověka vnímá každé vychýlení z rovnováhy a posílá informace do mozku. Mozek informace vyhodnotí a pošle zprávu do svalového aparátu k úpravě rovnováhy; dochází tak k neustálým opravám systému jezdec – kolo právě na základě zpětné vazby. | + | Složité systémy fungují jako celek; jejich chování je řízeno cyklickým vzorcem informací, kterému říkáme '''zpětnovazební smyčka'''. V praxi to znamená, že jedna část systému ovlivňuje systém jako celek a systém může zpětně onu část ovlivňovat a vzniká tak nová kvalita. Příkladem může být jízda na kole – rovnovážný aparát člověka vnímá každé vychýlení z rovnováhy a posílá informace do mozku. Mozek informace vyhodnotí a pošle zprávu do svalového aparátu k úpravě rovnováhy; dochází tak k neustálým opravám systému jezdec – kolo právě na základě zpětné vazby.<ref name="systémová dynamika model">MILDEOVÁ, Stanislava, 2011. Systémová dynamika: tvorba modelu. Praha: Oeconomica. ISBN 978-802-4518-428. |
| − | Ve výše uvedeném příkladu se jedná o '''negativní zpětnou vazbu''', vede ke stabilitě a rovnováze tím, že neguje změny; rozlišujeme také '''pozitivní (růstovou) zpětnou vazbu''', kdy se jedná o tzv. sebeposilující chování, protože způsobuje exponenciální růst v systému. Příkladem může být bankovní účet se stabilní úrokovou mírou, kdy při zvýšení množství peněz na bankovním účtu dochází ke zvýšení vyplaceného úroku, a tím zpětně ke zvýšení celkového množství peněz na bankovním účtu. | + | </ref> |
| − | Tento přístup se značně liší od tradičního analytického uvažování, které je především lineární – u modelů komplexních systémů je nezbytné celý proces chápat jako cyklickou smyčku (iterace), ne jako lineární závislost. | + | |
| + | Ve výše uvedeném příkladu se jedná o '''negativní zpětnou vazbu''', vede ke stabilitě a rovnováze tím, že neguje změny; rozlišujeme také '''pozitivní (růstovou) zpětnou vazbu''', kdy se jedná o tzv. sebeposilující chování, protože způsobuje exponenciální růst v systému. Příkladem může být bankovní účet se stabilní úrokovou mírou, kdy při zvýšení množství peněz na bankovním účtu dochází ke zvýšení vyplaceného úroku, a tím zpětně ke zvýšení celkového množství peněz na bankovním účtu.<ref name="ambroz">AMBROŽ, Ondřej, 2015. Systémová dynamika v projektech řízení kvality. Praha. Diplomová práce. Vysoká škola ekonomická v Praze.</ref> | ||
| + | |||
| + | {| class="wikitable" width="650" style="margin-left: 1em; margin-left: auto; margin-right: auto; border: none;" | ||
| + | |+ Příklady zpětných vazeb | ||
| + | |- | ||
| + | | style="padding-left: 1em; padding-right: 1em;" | [[File:pozitivni_vazba.png|thumb|centre|175 px|Pozitivní zpětná vazba]] | ||
| + | | style="padding-left: 1em; padding-right: 1em;" |[[File:negativni_vazba.png|thumb|centre|300 px|Negativní zpětná vazba]] | ||
| + | |- | ||
| + | | V případě, že stát A navýší výdaje na obranu a výzbroj, zvýší se tak potenciální hrozba vůči ostatním státům; toto donutí stát B také navýšit výdaje na obranu a zvýšit svoji vojenskou sílu. | ||
| + | | Tento systém je znázorněn pomocí dvou smyček počet nově narozených obyvatel zvyšuje celkovou populaci, počet úmrtí ji naopak snižuje, dochází tak k vyrovnání celého systému. | ||
| + | |} | ||
| + | |||
| + | Tento přístup se značně liší od tradičního analytického uvažování, které je především lineární – u modelů komplexních systémů je nezbytné celý proces chápat jako cyklickou smyčku (iterace), ne jako lineární závislost.<ref name="kirkwood">[http://www.public.asu.edu/~kirkwood/sysdyn/SDIntro/preface.pdf KIRKWOOD, Craig, 1998. System Dynamics Methods: A quick introduction. Arizona State University.]</ref> | ||
| + | |||
| + | {| class="wikitable" width="650" style="margin-left: 1em; margin-left: auto; margin-right: auto; border: none;" | ||
| + | | | ||
| + | |- | ||
| + | | style="padding-left: 1em; padding-right: 1em;" | [[File:linear.png|thumb|centre|150 px|Analytické myšlení]] | ||
| + | | style="padding-left: 1em; padding-right: 1em;" |[[File:loop.png|thumb|centre|150 px|Systémové myšlení]] | ||
| + | |- | ||
| + | | Standardní analytické myšlení spočívá v kauzální linearitě příčin a následků chování systému. V tomto případě události A a B jsou příčinou pro vznik událostí C a následně D. | ||
| + | | Systémové myšlení naopak chápe příčinu a následek jako cyklus vzájemně propojených událostí, kdy klíčové příčiny vycházejí z celkového chování systému. | ||
| + | |} | ||
| − | ===Modely systémové dynamiky=== | + | |
| + | ===Modely systémové dynamiky <ref name="systémová dynamika model">MILDEOVÁ, Stanislava, 2011. Systémová dynamika: tvorba modelu. Praha: Oeconomica. ISBN 978-802-4518-428. | ||
| + | </ref>=== | ||
Cílem systémové dynamiky je tvorba modelů - model představuje grafické, matematické, verbální či jiné zjednodušení komplexního systému. V systémové dynamice rozdělujeme dva typy modelů: | Cílem systémové dynamiky je tvorba modelů - model představuje grafické, matematické, verbální či jiné zjednodušení komplexního systému. V systémové dynamice rozdělujeme dva typy modelů: | ||
| Line 63: | Line 95: | ||
##Optimalizační modely, jejichž cílem je nalézt optimální řešení, většinou maximum nebo minimum. | ##Optimalizační modely, jejichž cílem je nalézt optimální řešení, většinou maximum nebo minimum. | ||
##Simulační modely, jejichž cílem je napodobit chování určitého systému tak, abychom jej mohli lépe poznat. | ##Simulační modely, jejichž cílem je napodobit chování určitého systému tak, abychom jej mohli lépe poznat. | ||
| + | |||
| + | ===Systémové archetypy<ref name="systémová dynamika model">MILDEOVÁ, Stanislava, 2011. Systémová dynamika: tvorba modelu. Praha: Oeconomica. ISBN 978-802-4518-428.</ref>=== | ||
| + | ::''Podrobnější informace naleznete na stránce [http://www.simulace.info/index.php/System_Archetypes/cs Systémové archetypy]'' | ||
| + | Jeden z nejdůležitějších postřehů z oblasti systémové dynamiky je ten, že mnoho dynamických smyček se pohybuje v určitých strukturách, které se znovu a znovu vrací; tyto struktury, neboli archetypy cohvání, odhalují jednoduchost, která se skrývá za zdánlivou komplexností velkých systémů. Systémová dynamika rozlišuje 11 základních archetypů, mezi nejznámější patří archetyp [http://www.simulace.info/index.php/Limits_to_Growth/cs "Meze růstu"], [http://www.simulace.info/index.php?title=Succes_to_the_Successful/cs&action=edit&redlink=1 "Úspěch úspěšným"] a [http://www.simulace.info/index.php?title=Tragedy_of_the_commons/cs&action=edit&redlink=1 "Tragédie obecní pastviny"]. | ||
| + | |||
=Základní diagramy systémové dynamiky= | =Základní diagramy systémové dynamiky= | ||
Mezi základní diagramy, které slouží pro popis systémů, patří diagram kauzálních smyček a diagram stavů a toků. | Mezi základní diagramy, které slouží pro popis systémů, patří diagram kauzálních smyček a diagram stavů a toků. | ||
| − | ===Diagram kauzálních smyček=== | + | ===Diagram kauzálních smyček <ref name="ambroz">AMBROŽ, Ondřej, 2015. Systémová dynamika v projektech řízení kvality. Praha. Diplomová práce. Vysoká škola ekonomická v Praze.</ref>=== |
| + | ::''Podrobnější informace naleznete na stránce [http://www.simulace.info/index.php/Causal_Loop_Diagram/cs Diagram kauzálních smyček] '' | ||
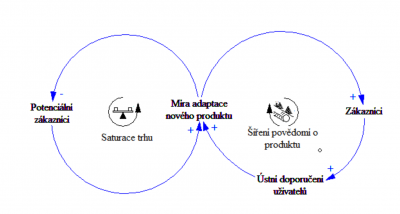
Smyčkový diagram představuje mentální model komplexního systému a zachycuje vzájemné propojení jednotlivých komponent systému. Základním stavebním kamenem je právě zpětná vazba (viz výše), pozitivní či negativní, která je znázorněna znaménky + a – nad šipkami, které propojují jednotlivé konstanty systému. V případě, že systém reaguje se zpožděním, je tento fakt znázorněn dvojitým přeškrtnutím šipky. Diagram tak umožňuje simulovat chování celého systému v čase. | Smyčkový diagram představuje mentální model komplexního systému a zachycuje vzájemné propojení jednotlivých komponent systému. Základním stavebním kamenem je právě zpětná vazba (viz výše), pozitivní či negativní, která je znázorněna znaménky + a – nad šipkami, které propojují jednotlivé konstanty systému. V případě, že systém reaguje se zpožděním, je tento fakt znázorněn dvojitým přeškrtnutím šipky. Diagram tak umožňuje simulovat chování celého systému v čase. | ||
| + | |||
| + | [[File:smyckovy_diagram.png|400 px]] | ||
===Diagram stavů a toků=== | ===Diagram stavů a toků=== | ||
| + | ::''Podrobnější informace naleznete na stránce [http://www.simulace.info/index.php/Stock_and_Flow_Diagram/cs Diagram stavů a toků] '' | ||
Svojí podstatou tvoří tento diagram základ simulačního modelu a v principu představuje detailnější pohled na modelovaný problém a vyhýbá se interpretačním problémům (ve srovnání s diagramem kauzálních smyček). Tento diagram je využíván zejména pro počítačové simulace, jeho transformací z diagramu kauzálních smyček je možné chování systému kvantifikovat. | Svojí podstatou tvoří tento diagram základ simulačního modelu a v principu představuje detailnější pohled na modelovaný problém a vyhýbá se interpretačním problémům (ve srovnání s diagramem kauzálních smyček). Tento diagram je využíván zejména pro počítačové simulace, jeho transformací z diagramu kauzálních smyček je možné chování systému kvantifikovat. | ||
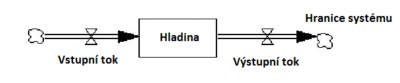
'''Stav''' je typ proměnné, která akumuluje změny; '''tok''' představuje stavební blok, který ovlivňuje stavy. Zatímco stavové proměnné představují statické kvantitativní množství, tokové proměnné jsou měřeny v určitém časovém rámci. Stav si lze představit jako stav hladiny vody ve vaně, která kumuluje tok vody z kohoutku. | '''Stav''' je typ proměnné, která akumuluje změny; '''tok''' představuje stavební blok, který ovlivňuje stavy. Zatímco stavové proměnné představují statické kvantitativní množství, tokové proměnné jsou měřeny v určitém časovém rámci. Stav si lze představit jako stav hladiny vody ve vaně, která kumuluje tok vody z kohoutku. | ||
| − | Konkrétní notace diagramu je závislá na zvoleném počítačovém editoru, mezi nejrozšířenější patří '''Powersim a Vensim'''. | + | Konkrétní notace diagramu je závislá na zvoleném počítačovém editoru, mezi nejrozšířenější patří '''[http://www.powersim.com Powersim] a [http://www.vensim.com Vensim]'''. |
[[File:stavy_toky.png|400 px|Diagram stavů a toků]] | [[File:stavy_toky.png|400 px|Diagram stavů a toků]] | ||
| Line 82: | Line 123: | ||
=Aplikace systémové dynamiky= | =Aplikace systémové dynamiky= | ||
| − | Principy systémové dynamiky je možné aplikovat všude, kde existuje nějaký systém, jehož chování chceme pochopit – existuje tedy široká škála projektů, na které je možné tento přístup aplikovat. Průkopníkem v tomto oboru je '''System Dynamics Society''', nezisková organizace se sídlem v New Yorku, která mj. shromažďuje reálně řešené problémy a angažuje se v rozvoji a výzkumu systémové dynamiky. Každý příklad je kategorizován dle sféry (komerční, nezisková, státní), sektoru (letectví, zdravotnictví, vzdělávání apod.) a oblasti zájmu (finance, HR, logistika, řízení kvality atd.). Jeden z příkladů popisuje řešení problému, kdy se USA potýkaly s vysokým počtem zubních kazů u dětí ve věku do 6 let, i přesto, že vynaložily značné finanční prostředky na jejich prevenci. Skrze analýzu dopadů jednotlivých politik zjistili, že účinnější řešení je vynaložit finanční prostředky na propagaci prevence u dětí všech věkových kategorií, než jejich vynaložení na nejohroženější skupiny. | + | Principy systémové dynamiky je možné aplikovat všude, kde existuje nějaký systém, jehož chování chceme pochopit – existuje tedy široká škála projektů, na které je možné tento přístup aplikovat. Průkopníkem v tomto oboru je '''[https://www.systemdynamics.org System Dynamics Society]''', nezisková organizace se sídlem v New Yorku, která mj. shromažďuje [http://cases.systemdynamics.org/list-of-all-cases/ reálně řešené problémy] a angažuje se v rozvoji a výzkumu systémové dynamiky. Každý příklad je kategorizován dle sféry (komerční, nezisková, státní), sektoru (letectví, zdravotnictví, vzdělávání apod.) a oblasti zájmu (finance, HR, logistika, řízení kvality atd.). |
| + | |||
| + | Jeden z příkladů popisuje řešení problému, kdy se USA potýkaly s vysokým počtem zubních kazů u dětí ve věku do 6 let, i přesto, že vynaložily značné finanční prostředky na jejich prevenci. Skrze analýzu dopadů jednotlivých politik zjistili, že účinnější řešení je vynaložit finanční prostředky na propagaci prevence u dětí všech věkových kategorií, než jejich vynaložení na nejohroženější skupiny. <ref name="oral_health">[http://cases.systemdynamics.org/exploring-prevention-strategies-for-improving-childrens-oral-health/ System Dynamics Case Repository: Children’s Oral Health, 2013. System Dynamics Society, New York] | ||
| + | </ref> | ||
=Příklady a procvičení= | =Příklady a procvičení= | ||
| + | |||
| + | #Zkuste vytvořit vlastní diagram kauzálních smyček pro váš pracovní či školní život. Řešení může vypadat např. [http://www.simulace.info/index.php/File:Myworklife.png i takto]. | ||
| + | #V úvodu textu jsou popsány příklady zdánlivě paradoxního chování sociálních systémů. Jak by se dalo toto výsledné chování vysvětlit v jednotlivých případech? | ||
| + | #Jaké jsou charakteristiky komplexních systémů? | ||
=Reference= | =Reference= | ||
| − | --[[User:Xzukm00|Xzukm00]] ([[User talk:Xzukm00|talk]]) | + | <references/> |
| + | |||
| + | --[[User:Xzukm00|Xzukm00]] ([[User talk:Xzukm00|talk]]) 21:45, 9 June 2017 (CEST) | ||
Latest revision as of 20:45, 9 June 2017
Contents
Úvod
Systémová dynamika je prakticky orientovaná disciplína pro studium chování komplexních sociálních systémů, která zdůrazňuje vztah mezi strukturou těchto systémů a výsledným chováním. Systémová dynamika se snaží objevovat v komplexních systémech určité vzory chování, které je možno zobecnit do podoby tzv. archetypů. Tyto vzorce chování jsou modelovány pomocí systému vnitřních smyček, zpětných vazeb a časových prodlev. Mezi hlavní přínosy této vědní disciplíny je možné zařadit schopnost modelovat skutečný svět, schopnost pojmout složitosti a vazby na zpětné struktury, které jsou v těchto sociálních systémech; nezbytné je také využití počítačových modelů a simulací – jádrem systémové dynamiky je vytváření explicitních modelů.[1]
Vznik systémové dynamiky je spojován s řešením reálné situace, která nastala ve firmě General Electrics v 50. letech 20. století – společnost nemohla vyřešit stále opakující se problém, kdy dělníci museli v jednom roce pracovat na tři, nebo čtyři směny a v dalším roce bylo nutné polovinu dělníků propustit. Vedení společnosti přisuzovalo tyto výkyvy změnám v ekonomickém cyklu a v poptávce, nicméně pomocí počítačových simulací zjistili, že vztah mezi objednávkami, skladovými zásobami a zaměstnaností spočívá ve vnitřní determinovanosti systému, tedy politikách, podle kterých se rozhodovalo – celý systém byl ovlivněn faktory, které vedení společnosti vůbec původně nevzalo v potaz. [1]
K podobným reakcím dochází v komplexních systémech neustále – Spojené státy americké celoročně vydají na zdravotní péči více než jakákoli jiná země na světě (v absolutní výši i poměrně k HDP), ale i přesto více než 40 milionů obyvatel nemá zdravotní pojištění, a Spojeným státům zároveň patří spodní příčky mezi vyspělými zeměmi z hlediska průměrné délky života a kojenecké úmrtnosti; komplexní výstavby nových dálnic za účelem snížení hustoty dopravy ve špičkách naopak dopravu ztěžují a zhoršují znečištění a kvalitu životního prostředí; antibiotika a nové léky urychlily evoluci rezistentních bakterií a patogenů, agresivní pesticidy a herbicidy podpořily vývoj odolných odrůd plevele a hmyzu, vyhubily přirozené predátory a často stojí za otravou ryb, ptáků a jiných živočichů. Toto zdánlivé paradoxní chování systémů je cílem zkoumání systémové dynamiky. [2]
Historie systémové dynamiky
| Jay Wright Forrester |
|---|
|
Systémová (původně průmyslová) dynamika byla založena profesorem J. W. Forresterem ze Sloan School of Management na Massachusetts Institute of Technology. První článek týkající se této nové vědní disciplíny byl publikován v roce 1958, později využit jako druhá kapitola knihy od téhož autora „Industrial Dynamics“ z roku 1961. Na konci 50. let byl vyvinut první formální počítačový jazyk pro tvorbu modelů a simulací SIMPLE (Simulation of Industrial Management Probems with Lots of Equations), jehož autorem je Richard Bennett. Až do konce 60. let 20. století byla Systémová dynamika aplikována téměř výhradně na řešení manažerských problémů (60. léta byla charakteristická stagnací či bankrotem velkého množství technologických firem, které zprvu velmi rychle rostly – na základě tohoto fenoménu vznikl jeden ze základních systémových archetypů, model mezí růstu (Limits to Growth)). [3]
V roce 1968 se Systémová dynamika rozšířila díky spolupráci J. Forrestera a Johna Collinse, bývalého starosty Bostonu, i do oblasti urbanistiky a urbanistického rozvoje. Tato část vědy se zabývala zjištěním příčin toho, proč vznikají ve městech oblasti s vysokou mírou kriminality. Kniha Urban Dynamics, která vzešla z analýzy těchto poznatků, vedla právě ke zjištění, že některé základní politiky na zlepšení životní úrovně obyvatelstva jsou kontraproduktivní a byla ve své době považována téměř za kontroverzní dílo.
S postupným rozvojem počítačů a systémových modelů docházelo k rozvoji nástrojů pro dynamické modelování – simulační jazyk DYNAMO, simulační software Vensim, Powersim a STELLA; od 70. let bylo systematické modelování zejména v USA značně rozšířeno, a to i například na oblast projektového managementu.[3]
V České republice se využití systémové dynamiky rozvíjelo od 70. let zejména v univerzitním prostředí, poté až od roku 1995 i v komerčních sférách a státním sektoru; dynamické modelování bylo využito např. pro podporu plánování v Českém Telecomu, pro Armádu ČR byl vytvořen personalistický model, který obsahoval mj. demografii, trh pracovních sil a mobilitu pracovních sil. Ve všech výše uvedených příkladech byly modely použity pro získání prvotního vhledu do problematiky – poznání endogenní smyčkové zpětnovazební struktury příčin a následků, která vede k problémovému chování komplexního systému. Na základě těchto informací bylo možné ověřit logické důsledky a dopad rozhodnutí na celý systém.[1]
Základní koncepty systémové dynamiky
Komplexní systémy[1]
Před vlastním vymezením oblasti zájmu systémové dynamiky je nutné pochopit, kterými systémy se zabývá; komplexní systém představuje uskupení vzájemně propojených a ovlivňujících se prvků, které tvoří celek a má následující základní charakteristiky[4]:
- Vzájemná závislost (interdipendence) – čím více jsou na sobě prvky závislé, tím méně je možné pochopit chování systému pouze na základě pochopení jednotlivých prvků.
- Pozitivní a negativní zpětné vazby – jde o situace, kdy jev a způsobí následný jev b, který zpětně ovlivní jev a. Existují dva typy zpětné vazby – pozitivní (působí ve stejném směru k původnímu jevu) a negativní (působí v protisměru k původnímu jevu – čím více a, tím více b a čím více b, tím méně a) – viz níže.
- Detailní a dynamická složitost – i systém s malým množstvím prvků dokáže generovat velmi složité chování. Důležitým fenoménem je také vliv zpoždění (materiální či informační), které způsobuje velké množství nepříjemných efektů, např. zakrytí kauzálních vztahů, kdy je pravá příčina nezpozorována, způsobuje problémy při získávání informací o aktuálním stavu systému apod.
- Nelinearita – systémové chování neodpovídá přímé úměře; není vždy příliš účinné působit intuitivně nástroji, které přímo ovlivňují požadovaný parametr, protože systém se často postaví proti směru působení.
- Nejistota – nejsme schopni postihnou všechny možnosti a pravděpodobnosti vývoje systému.
- Neurčitost – situace, kdy známe všechna možná východiska včetně pravděpodobností, ale nevíme, co konkrétně nastane.
Chování komplexních systémů je možné poznat skrze jejich strukturu, která toto chování determinuje. Pokud se nám podaří poznat klíčové komponenty včetně zpětnovazebních souvislostí, budeme schopni nalézt postupy, které povedou k zajištění cílového chování systému.
Zpětná vazba
Složité systémy fungují jako celek; jejich chování je řízeno cyklickým vzorcem informací, kterému říkáme zpětnovazební smyčka. V praxi to znamená, že jedna část systému ovlivňuje systém jako celek a systém může zpětně onu část ovlivňovat a vzniká tak nová kvalita. Příkladem může být jízda na kole – rovnovážný aparát člověka vnímá každé vychýlení z rovnováhy a posílá informace do mozku. Mozek informace vyhodnotí a pošle zprávu do svalového aparátu k úpravě rovnováhy; dochází tak k neustálým opravám systému jezdec – kolo právě na základě zpětné vazby.[5]
Ve výše uvedeném příkladu se jedná o negativní zpětnou vazbu, vede ke stabilitě a rovnováze tím, že neguje změny; rozlišujeme také pozitivní (růstovou) zpětnou vazbu, kdy se jedná o tzv. sebeposilující chování, protože způsobuje exponenciální růst v systému. Příkladem může být bankovní účet se stabilní úrokovou mírou, kdy při zvýšení množství peněz na bankovním účtu dochází ke zvýšení vyplaceného úroku, a tím zpětně ke zvýšení celkového množství peněz na bankovním účtu.[3]
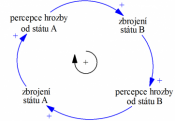
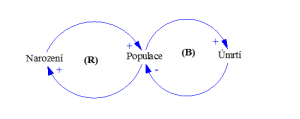
| V případě, že stát A navýší výdaje na obranu a výzbroj, zvýší se tak potenciální hrozba vůči ostatním státům; toto donutí stát B také navýšit výdaje na obranu a zvýšit svoji vojenskou sílu. | Tento systém je znázorněn pomocí dvou smyček počet nově narozených obyvatel zvyšuje celkovou populaci, počet úmrtí ji naopak snižuje, dochází tak k vyrovnání celého systému. |
Tento přístup se značně liší od tradičního analytického uvažování, které je především lineární – u modelů komplexních systémů je nezbytné celý proces chápat jako cyklickou smyčku (iterace), ne jako lineární závislost.[4]
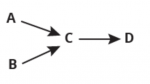
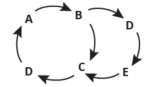
| Standardní analytické myšlení spočívá v kauzální linearitě příčin a následků chování systému. V tomto případě události A a B jsou příčinou pro vznik událostí C a následně D. | Systémové myšlení naopak chápe příčinu a následek jako cyklus vzájemně propojených událostí, kdy klíčové příčiny vycházejí z celkového chování systému. |
Modely systémové dynamiky [5]
Cílem systémové dynamiky je tvorba modelů - model představuje grafické, matematické, verbální či jiné zjednodušení komplexního systému. V systémové dynamice rozdělujeme dva typy modelů:
- Mentální modely, které představují vnitřní reprezentaci okolního světa a vztahů mezi různými jeho částmi, které lidé vytváří, často jsou velmi zjednodušené.
- Počítačové modely, které jsou srozumitelné, snadno komunikovatelné a mohou brát v úvahu více faktorů najednou, na druhou stranu nepředstavují přesnou realitu (jsou zjednodušené) a k jejich tvorbě jsou nezbytná kvantifikovaná data. Lze je rozdělit do dvou základních kategorií:
- Optimalizační modely, jejichž cílem je nalézt optimální řešení, většinou maximum nebo minimum.
- Simulační modely, jejichž cílem je napodobit chování určitého systému tak, abychom jej mohli lépe poznat.
Systémové archetypy[5]
- Podrobnější informace naleznete na stránce Systémové archetypy
Jeden z nejdůležitějších postřehů z oblasti systémové dynamiky je ten, že mnoho dynamických smyček se pohybuje v určitých strukturách, které se znovu a znovu vrací; tyto struktury, neboli archetypy cohvání, odhalují jednoduchost, která se skrývá za zdánlivou komplexností velkých systémů. Systémová dynamika rozlišuje 11 základních archetypů, mezi nejznámější patří archetyp "Meze růstu", "Úspěch úspěšným" a "Tragédie obecní pastviny".
Základní diagramy systémové dynamiky
Mezi základní diagramy, které slouží pro popis systémů, patří diagram kauzálních smyček a diagram stavů a toků.
Diagram kauzálních smyček [3]
- Podrobnější informace naleznete na stránce Diagram kauzálních smyček
Smyčkový diagram představuje mentální model komplexního systému a zachycuje vzájemné propojení jednotlivých komponent systému. Základním stavebním kamenem je právě zpětná vazba (viz výše), pozitivní či negativní, která je znázorněna znaménky + a – nad šipkami, které propojují jednotlivé konstanty systému. V případě, že systém reaguje se zpožděním, je tento fakt znázorněn dvojitým přeškrtnutím šipky. Diagram tak umožňuje simulovat chování celého systému v čase.
Diagram stavů a toků
- Podrobnější informace naleznete na stránce Diagram stavů a toků
Svojí podstatou tvoří tento diagram základ simulačního modelu a v principu představuje detailnější pohled na modelovaný problém a vyhýbá se interpretačním problémům (ve srovnání s diagramem kauzálních smyček). Tento diagram je využíván zejména pro počítačové simulace, jeho transformací z diagramu kauzálních smyček je možné chování systému kvantifikovat. Stav je typ proměnné, která akumuluje změny; tok představuje stavební blok, který ovlivňuje stavy. Zatímco stavové proměnné představují statické kvantitativní množství, tokové proměnné jsou měřeny v určitém časovém rámci. Stav si lze představit jako stav hladiny vody ve vaně, která kumuluje tok vody z kohoutku. Konkrétní notace diagramu je závislá na zvoleném počítačovém editoru, mezi nejrozšířenější patří Powersim a Vensim.
Aplikace systémové dynamiky
Principy systémové dynamiky je možné aplikovat všude, kde existuje nějaký systém, jehož chování chceme pochopit – existuje tedy široká škála projektů, na které je možné tento přístup aplikovat. Průkopníkem v tomto oboru je System Dynamics Society, nezisková organizace se sídlem v New Yorku, která mj. shromažďuje reálně řešené problémy a angažuje se v rozvoji a výzkumu systémové dynamiky. Každý příklad je kategorizován dle sféry (komerční, nezisková, státní), sektoru (letectví, zdravotnictví, vzdělávání apod.) a oblasti zájmu (finance, HR, logistika, řízení kvality atd.).
Jeden z příkladů popisuje řešení problému, kdy se USA potýkaly s vysokým počtem zubních kazů u dětí ve věku do 6 let, i přesto, že vynaložily značné finanční prostředky na jejich prevenci. Skrze analýzu dopadů jednotlivých politik zjistili, že účinnější řešení je vynaložit finanční prostředky na propagaci prevence u dětí všech věkových kategorií, než jejich vynaložení na nejohroženější skupiny. [6]
Příklady a procvičení
- Zkuste vytvořit vlastní diagram kauzálních smyček pro váš pracovní či školní život. Řešení může vypadat např. i takto.
- V úvodu textu jsou popsány příklady zdánlivě paradoxního chování sociálních systémů. Jak by se dalo toto výsledné chování vysvětlit v jednotlivých případech?
- Jaké jsou charakteristiky komplexních systémů?
Reference
- ↑ 1.0 1.1 1.2 1.3 MILDEOVÁ, Stanislava a Viktor VOJTKO, 2003. Systémová dynamika. V Praze: Oeconomica. ISBN 80-245-0626-2.
Cite error: Invalid
<ref>tag; name "systémová dynamika" defined multiple times with different content - ↑ STERMAN, John, 2001. System Dynamics Modeling: TOOLS FOR LEARNING IN A COMPLEX WORLD. University of California.
- ↑ 3.0 3.1 3.2 3.3 AMBROŽ, Ondřej, 2015. Systémová dynamika v projektech řízení kvality. Praha. Diplomová práce. Vysoká škola ekonomická v Praze.
- ↑ 4.0 4.1 KIRKWOOD, Craig, 1998. System Dynamics Methods: A quick introduction. Arizona State University.
- ↑ 5.0 5.1 5.2 MILDEOVÁ, Stanislava, 2011. Systémová dynamika: tvorba modelu. Praha: Oeconomica. ISBN 978-802-4518-428.
Cite error: Invalid
<ref>tag; name "systémová dynamika model" defined multiple times with different content - ↑ System Dynamics Case Repository: Children’s Oral Health, 2013. System Dynamics Society, New York