Difference between revisions of "N-player prisoner's dilemma/cs"
FrantišekN (talk | contribs) |
FrantišekN (talk | contribs) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 58: | Line 58: | ||
=== N-Player Prisoner’s Dilemma in Multiple Groups: A Model of Multilevel Selection === | === N-Player Prisoner’s Dilemma in Multiple Groups: A Model of Multilevel Selection === | ||
| − | Na vytvořeném modelu dvou soupeřících skupin, ve kterých současně probíhá soupeření vnitroskupinové je prezentována přechodná emergence Simpsonova paradoxu. Relativní podíl spolupracujících může jednotlivě v obou skupinách klesat a současně v rámci celé populace agentů růst. Skupiny mají stejný výchozí počet agentů, kteří mezi nimi nemohou přecházet. Jednotlivé agenty mají zjednodušené strategie, buď vždy spolupracují, nebo vždy nespolupracují. | + | Na vytvořeném modelu dvou soupeřících skupin, ve kterých současně probíhá soupeření vnitroskupinové je prezentována přechodná emergence Simpsonova paradoxu. Relativní podíl spolupracujících může jednotlivě v obou skupinách klesat a současně v rámci celé populace agentů růst. Skupiny mají stejný výchozí počet agentů, kteří mezi nimi nemohou přecházet. Jednotlivé agenty mají zjednodušené strategie, buď vždy spolupracují, nebo vždy nespolupracují. Užitkové funkce ze spolupráce a nespolupráce je v rámci každé ze skupin v závislosti na podílu spolupracujících vůči celku. Jsou opět v rámci zjednodušení lineární a paralelní. Prvním definujícím parametrem je strmost, čím větší, tím více má skupina větší užitek z každého dalšího spolupracujícího agenta. Druhý parametr určuje nárůst užitku pramenící z nespolupráce (posun funkce nespolupráce po ose užitku y oproti funkci spolupráce). Pro každou jednotku času běhu modelu je navýšen počet spolupracujících agentů v závislosti na užitku spolupracujících vůči podílu spolupracujících ve skupině a obdobně počet nespolupracujících v závislosti na užitku nespolupracujících vůči podílu nespolupracujících ve skupině. Výsledný nový poměr spolupracujících a nespolupracujících ve skupině je přenesen na výchozí počet agentů ve skupině, který tak zůstává neměnný. Studie dokládá emergenci Simpsonova paradoxu a zkoumá, za jakých výchozích podmínek se v modelu přechodně objevuje a jaký má průběh. Výsledky jsou interpretovány ve vztahu ke vzniku a růstu altruistického chování.<ref>Fletcher, Jeffrey and Zwick, Martin. N-Player Prisoner’s Dilemma in Multiple Groups: A Model of Multilevel Selection, 2000. [cit. 2017-06-04]. Dostupné z: https://www.pdx.edu/sites/www.pdx.edu.sysc/files/sysc_alife7.pdf</ref> |
| Line 98: | Line 98: | ||
| − | ''' | + | '''Vyplatí se agentu ve specifické situaci, ve které všechny ostatní agenty budou volit strategii spolupráce, nespolupracovat?
''' |
a) ano <span style="color: white">SPRÁVNĚ</span> | a) ano <span style="color: white">SPRÁVNĚ</span> | ||
Latest revision as of 13:29, 9 June 2017
Contents
Úvod
Rozšíření Vězňova dilematu, ikonického problému z Teorie her, ze dvou na n-hráčů umožňuje jeho aplikaci pro modelování většího množství reálných situací, kde zpravidla dochází k interakcím více subjektů. Typicky jde o sociální systémy a problematiku kolektivního chování. Do Vězňova dilematu více hráčů se přenáši charakteristiky původního problému:
- Účastníci se nachází v nějaké situaci, kde mají možnost buď spolupracovat, nebo nespolupracovat (zradit ostatní pro zvýšení osobního užitku).
- Nehledě na to, jak se rozhodnou ostatní subjekty, pro užitek každého jednotlivě je nejvýhodnější nespolupracoat a zradit.
- Současně ale platí, že pokud všechny subjekty zvolí možnost nespolupracovat, užitek každého z nich je nižší, než kdyby se všechny subjekty rozhodly spolupracovat.
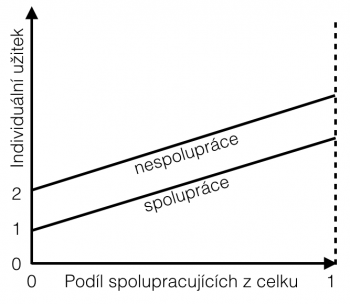
Dominantnost strategie nespolupráce nad spoluprácí, nehledě na celkový podíl spolupracujících z celku, ukazuje vzájemné postavení křivek funkcí spolupráce a nespolupráce v grafu. Konkrétní podoba křivek funkcí závisí na definici problému.
Podstatou dilematu je tedy, že individuální racionalita vede ke kolektivní iracionalitě. Nashova rovnováha spočívá v hromadné nespolupráci. G.Hardin Vězňovo dilema pro více hráčů trefně a vtipně charakterizuje jako “Matematickou formulaci toho, co je špatně s naší společností”.[1]
Subjekty interagující ve Vězňově dilematu jsou označovány jako agenty a mohou to být například jednotlivci, skupiny lidí, korporace, nebo počítačové programy.
Definující parametry
Kromě užitku ze spolupráce a nespolupráce pro všechny možné poměry spolupracujících a nespolupracujících agentů je možno v rámci definice uvážit řadu dalších určujících faktorů.
Agenty se mohou, ale nemusejí rozhodovat ve stejném čase, za stejných výchozích podmínek a mohou, ale nemusejí mít k dispozici informaci o tom, jak se rozhodují ostatní. Pokud mají možnost a schopnost mezi sebou komunikovat, mohou například tvořit koalice. Dále mohou mít různě definované cíle s kterými do hry Vězňova dilematu vstupují. Prostorové uspořádání může a nemusí hrát roli a může se i měnit. Z uspořádání mohou vycházet omezení, agenty například hrají vězňovo dilema jen v rámci svého přilehlého okolí. Hra může mít pouze jedno kolo, nebo řadu navazujících kol. U trvání a jeho konečnosti je opět důležité, zda jsou s ním agenty obeznámeny. Pokud mají hry dilematu více kol, agenty mohou rozhodování průběžně korigovat v závislosti na chování ostatních. Jakým způsobem, konceptualizuje Szilagyi[2] pomocí rozdělení na několik typů “osobností” agentů, které se mohou během hry dilematu i měnit.
- U Pavlovovské osobnosti se pravděpodobnost spolupráce, ev. nespolupráce mění proporčně ve vztahu k získanému užitku a eventuální penalizaci plynoucím z rozhodnutí. Agenty se tak průběžně “vychovávají” po vzoru behavioralistického cukru a biče.
- Stochasticky předvidatelné osobnosti se rozhodují stále stejným způsobem, bez ovlivňování z okolí. Například tedy vždy spolupracují, nebo nespolupracují, nebo vždy spolupracují s danou konstantní pravděpodobností.
- Konformistická osobnost volí rozhodnutí v souladu s většinou okolních agentů.
- Lakomá osobnost kopíruje rozhodnutí nejůspěšnějšího souseda.
- U osobnosti účetní pravděpodobnosti rozhodnutí pro spolupráci a nespolupráci vycházejí z průměrných užitků rozhodnutí za předchozí herní kola.
Další typy osobností je možné definovat pomocí abstrahování z reálných vlastností, které chceme v dilematu prozkoumat. Příkladem by třeba mohla být tvrdohlavá osobnost, která mění strategii neochotně, pomaleji, se setrvačností více kol. To ostatně platí i pro další dpoplňující parametry a jejich podrobnější a konkrétnější specifikace.
Příklady
Na jakých reálných příkladech a situacích lze Vězňovo dilema více hráčů vysledovat? Dobrým příkladem z historie je zbrojení a nukleární pat během studené války. Všechny zůčastněné strany se v čele s vedoucími mocnostmi USA a Sovětským svazem dostali do situace, kde přestat zbrojit bylo velmi problematické. Po zlepšení vztahů pak bylo nutno uzavřít dohody o jaderném odzbrojování.
Snad nejznámějším příkladem je Tragédie obecní pastviny, inspirovaná skutečnými poměry v osmnáctém století v Anglii. Představme si vzorovou situaci, kde šest pastevců sdílí malou kravskou pastvinu. Každý na ní ráno vodí jednu krávu, která se dobře pase a udržuje si váhu 1000 Kg. Každý pastevec má ale možnost přihnat na pastvinu dodatečnou krávu, všechny pasoucí krávy tak mají o něco méně potravy a v důsledku se jim za nějakou dobu sníží váha o 100 Kg. Pastevec, co si přivedl dodatečnou krávu má teď ale dvě krávy s celkovou hmotností 1800 Kg, výrazněže si tedy polepšil. Když to vidí ostatní pastevci, každý si na pastvinu přivede taky dodatečnou krávu. Celkem je pak na pastvině dvanáct krav, každá váží 400 Kg a všichni pastevci mají celkovou hmotnost 800 Kg oproti původním 1000 Kg.[3] Jako další krok lze očekávat, že pastevci budou řešit situaci přidáváním dalších kráv, což v konečné fázi povede k tragédii v podobě vyčerpání pastviny a vyhladovění dobytka. Jak situaci řešit a tragédii obecní pastviny předejít? Způsoby, které se dnes běžně uplatňují, to jest postihnutím nespolupráce (přidání další krávy na pastvinu) pomocí restrikcí a nařízení. Pastevci, kteří vědí, že za nespolupráci mohou být penalizováni ji už nevyhodnotí, jako výhodnou a zároveň tak dostanou jakýchsi záruk, že ostatní si další krávu na pastvinu také nepřivedou.
Aktuálním dnes a ještě více zítra, je problém s šetřením pitnou vodou. Jedná se o obdobu Tragédie obecní pastviny. S nastupujícím nedostatkem vyvstává potřeba šetřit. Šetření jednotlivce však nestačí, je nutné, aby se na něm podílelo velké množství lidí. Když ale šetří vodou skoro všichni, jednotlivec, který nešetří, nepředstavuje žádný znatelný rozdíl. Je tedy racionální se ve spotřebě vody i v tomto případě neomezovat. Pokud všichni dojdou k tomuto individuálnímu závěru a nebudou šetřit, vody bude akutní nedostatek, situace mnohem horší, než potřeba uskromnit se ve spotřebě. Obdobně můžeme vysledovat Vězňovo dilema více hráčů v nakládání s dalšími omezenými přírodními zdroji (ať už vyčerpatelnými, či pomalu obnovitelnými), například rybolov v mezinárodních vodách. Nebo i v nakládání s životním prostředím obecně, například znečištění a postoje ke globálnímu oteplování.
Vybrané studie
V následující části jsou souhrny tří vybraných studií zabývajících se různými aspekty Vězňova dilematu více hráčů.
Cognitive load in the multi-player prisoner's dilemma game: Are there brains in games?
Studie[4] předkládá výsledky uskutečněného experimentu, který měl za úkol zjistit vliv kognitivní zátěže na srategické uvažování, výkon a úspěšnost v simulované hře Vězňova dilematu o více hráčích. Účastnilo se ho celkem 48 studentů Rutgers University v Camden seskupených po neměnných čtveřicích, v rámci kterých proti sobě hráli 30 kol Vězňova dilematu. Užitek byl reprezentován ziskem bodů, které se nakonci experimentu převedly na utržené dolary. Dalším motivačním prvkem byl pro účastníky vstupní vklad do hry ve výši pěti dolarů. Studenti se v rámci svojí herní čtveřice neznali a byli po dobu trvání experimentu odděleni. Vězňovo dilema se hrálo pomocí jednoduchého programu na síti počítačů. Přidaná kognitivní zátěž byla realizována v podobě požadavku na zapamatování si přiděleného čísla v každém kole hry. U skupiny účastníků s nízkou zátěží šlo o dvouciferné číslo a u skupiny s vysokou zátěží o sedmiciferné. Studenti měli vždy 15s na zapamatování čísla, které měli na konci herního kola zopakovat. Bodový zisk byl podmíněn správností zopakovaného čísla. S počtem kol a pravidly byli účastníci předem seznámeni. Po třicátém kole každý student vyplnil krátký dotazník, kde pomocí škály vyjadřoval dojmy z experimentu. Výsledky experimentu potvrdili hypotézu, že rozdíl v dostupnosti kognitivních kapacit má vliv na strategické rozhodování. Obě skupiny s přibývajícími koly experimentu prokazovaly snižování ochoty volby strategie spolupracovat. Skupina s nižší přidanou kognitivní zátěží prokazovala více strategické nespolupráce v konečných kolech hry a byla obecně schopná lépe reagovat a upravovat rozhodování v závislosti na předchozích kolech hry. Studie nepotvrdila tendence více spolupracovat u hráčů s vyššími kognitivními schopnostmi, tak jak naznačuje výzkum [5], ve kterém skupiny studentů s rostoucím průměrným SAT score vykazují růst v četnostech rozhodnutí kooperovat. Autoři uvažují, že je to dáno rozdílným nastavením experimentu, zejména konečným a předem známým počtem kol.
N-Player Prisoner’s Dilemma in Multiple Groups: A Model of Multilevel Selection
Na vytvořeném modelu dvou soupeřících skupin, ve kterých současně probíhá soupeření vnitroskupinové je prezentována přechodná emergence Simpsonova paradoxu. Relativní podíl spolupracujících může jednotlivě v obou skupinách klesat a současně v rámci celé populace agentů růst. Skupiny mají stejný výchozí počet agentů, kteří mezi nimi nemohou přecházet. Jednotlivé agenty mají zjednodušené strategie, buď vždy spolupracují, nebo vždy nespolupracují. Užitkové funkce ze spolupráce a nespolupráce je v rámci každé ze skupin v závislosti na podílu spolupracujících vůči celku. Jsou opět v rámci zjednodušení lineární a paralelní. Prvním definujícím parametrem je strmost, čím větší, tím více má skupina větší užitek z každého dalšího spolupracujícího agenta. Druhý parametr určuje nárůst užitku pramenící z nespolupráce (posun funkce nespolupráce po ose užitku y oproti funkci spolupráce). Pro každou jednotku času běhu modelu je navýšen počet spolupracujících agentů v závislosti na užitku spolupracujících vůči podílu spolupracujících ve skupině a obdobně počet nespolupracujících v závislosti na užitku nespolupracujících vůči podílu nespolupracujících ve skupině. Výsledný nový poměr spolupracujících a nespolupracujících ve skupině je přenesen na výchozí počet agentů ve skupině, který tak zůstává neměnný. Studie dokládá emergenci Simpsonova paradoxu a zkoumá, za jakých výchozích podmínek se v modelu přechodně objevuje a jaký má průběh. Výsledky jsou interpretovány ve vztahu ke vzniku a růstu altruistického chování.[6]
An Investigation of N-person Prisoners’ Dilemmas
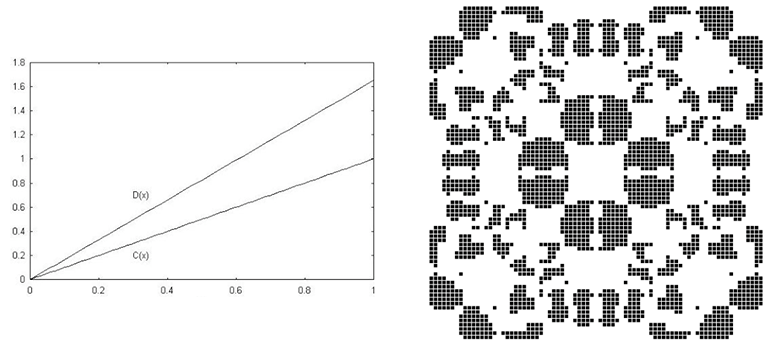
Článek v první části poskytuje úvod do problematiky Vězňova dilematu více hráčů a v části druhé prezentuje jeho vytvořený, agentní, stochastický model. Model je dvoudimenzionální a umožňuje podrobné nastavení řady vstupních parametrů, tak aby jej bylo možné aplikovat na simulace různých reálných situací. Jako příklad uvádím výstup z tisíctého kola hry kde ve výchozím postavení prostřední pole obsazoval lakomý, nespolupracující agent a všechna ostatní pole náležela lakomým spolupracujícím agentům. Hry dilematu probíhali mezi přilehlými sousedy. Užitkové křivky funkcí spolupráce (C(x)=x) a nespolupráce (D(x)=1.65x) jsou zaneseny v grafu. Černá pole značí spolupracující agenty a bílá nespolupracující.[7]
Otázky k procvičení
U následujících otázek vyberte vždy pouze jednu správnou odpověď:
Jaká je dominantní strategie racionálního agenta v jednokolové hře vězňova dilematu více hráčů?
a) spolupracovat
b) nespolupracovat SPRÁVNĚ
c) nelze určit
Co je klíčovou charakteristikou Tragédie obecní pastviny (Tragedy of the Commons) a odvozených problémů?
a) Řeší optimální rozmístění agentů (v tomto případě krav) v definované lokalitě.
b) Vystupuje v ní sdílený, omezený, vyčerpatelný zdroj. SPRÁVNĚ
c) Vůbec by k ní nedošlo, kdyby se účastníci chovali racionálně a správně maximalizovali svůj užitek.
Platí základní charakteristiky Vězňova dilematu pro více hráčů pro původní vězňovo dilema (2 hráči)?
a) ano SPRÁVNĚ
b) ne
c) nelze určit
Vyplatí se agentu ve specifické situaci, ve které všechny ostatní agenty budou volit strategii spolupráce, nespolupracovat?
a) ano SPRÁVNĚ
b) ne
c) nelze určit
| Označte text odstavce otázek pro odkrytí správných odpovědí! |
Reference
- ↑ G. Hardin, “The Tragedy of the Commons,” Science, 162 (1968) 1243– 1248.
- ↑ Szilagyi, Miklos N. "An investigation of N-Person prisoners' dilemmas." Complex Systems 14.2 (2003): 155-174.
- ↑ N-Person Prisoner's Dilemma. Stanford.edu [online]. [cit. 2017-06-09]. Dostupné z: https://cs.stanford.edu/people/eroberts/courses/soco/projects/1998-99/game-theory/npd.html
- ↑ Duffy, Sean and Smith, John, Cognitive Load in the Multi-Player Prisoner's Dilemma Game: Are There Brains in Games? [cit. 2017-06-04]. Dostupné z SSRN: https://ssrn.com/abstract=1841523 nebo http://dx.doi.org/10.2139/ssrn.1841523
- ↑ Jones, Garett. Are smarter groups more cooperative? Evidence from prisoner's dilemma experiments, 1959–2003. Journal of Economic Behavior & Organization [online]. 2008, 68(3-4), 489-497 [cit. 2017-06-04]. DOI: 10.1016/j.jebo.2008.06.010. ISSN 01672681. Dostupné z: http://linkinghub.elsevier.com/retrieve/pii/S0167268108001315
- ↑ Fletcher, Jeffrey and Zwick, Martin. N-Player Prisoner’s Dilemma in Multiple Groups: A Model of Multilevel Selection, 2000. [cit. 2017-06-04]. Dostupné z: https://www.pdx.edu/sites/www.pdx.edu.sysc/files/sysc_alife7.pdf
- ↑ Szilagyi, Miklos N. "An investigation of N-Person prisoners' dilemmas." Complex Systems 14.2 (2003): 155-174.