Difference between revisions of "Optimalizace nastavení eskalátorů v metru (NetLogo)"
(→Možná rozšíření modelu) |
(hotfix nesmyslné části textu) |
||
| (12 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
= Zadání = | = Zadání = | ||
| Line 18: | Line 9: | ||
'''Typ modelu''': Multiagentní | '''Typ modelu''': Multiagentní | ||
| − | '''Modelovací nástroj''': NetLogo | + | '''Modelovací nástroj''': NetLogo 5.3.1 |
= Definice problému = | = Definice problému = | ||
Simulace slouží k nalezení optimální rychlosti a počtu aktivních eskalátorů. Máme situaci s předem danými parametry. Do stanice přijede metro, vyloží cestující a ti jdou k nejbližšímu eskalátoru, přičemž pokud je eskalátorů více, zvolí si jeden z nich, jedoucí danou rychlostí. Někteří cestující jdou, a to po levé straně eskalátoru, někteří stojí na pravé straně. Ti inteligentnější stojí opravdu vpravo tak, aby nevadili těm, kteří chtějí jít. Ti, kterým Pán Bůh tolik nenadělil stojí vlevo, a tak blokují všechny za sebou. | Simulace slouží k nalezení optimální rychlosti a počtu aktivních eskalátorů. Máme situaci s předem danými parametry. Do stanice přijede metro, vyloží cestující a ti jdou k nejbližšímu eskalátoru, přičemž pokud je eskalátorů více, zvolí si jeden z nich, jedoucí danou rychlostí. Někteří cestující jdou, a to po levé straně eskalátoru, někteří stojí na pravé straně. Ti inteligentnější stojí opravdu vpravo tak, aby nevadili těm, kteří chtějí jít. Ti, kterým Pán Bůh tolik nenadělil stojí vlevo, a tak blokují všechny za sebou. | ||
| + | |||
| + | == Cíl == | ||
| + | |||
| + | Cílem je pomocí vytvořeného modelu minimalizovat počet aktivních eskalátorů, čímž dojde ke snížení nákladů, a minimalizovat dobu, kdy je eskalátor v provozu, což lze odhadnout podle toho, za jakou dobu se všichni dostanou ven z prostoru metra. | ||
= Metoda = | = Metoda = | ||
| Line 165: | Line 160: | ||
=== Výhody === | === Výhody === | ||
| − | * ... | + | * Model ukazuje výsledky v reálném čase nebo zrychleně, přičemž vždy zobrazuje skutečné hodnoty v sekundách. |
| + | * Je pokryt nejčastější stav na eskalátorech, a to včetně zastavení někoho v pohybující se řadě. | ||
| + | * Model umí kromě časů opuštění počítat i s náklady, což zvyšuje komfort uživateli. | ||
| + | * Model lze snadno rozšířit o nové zajímavé funkcionality | ||
| + | * V modelu lze snadno vyměnit rozdělení, ze kterých jsou generovány vlastnosti cestujících a eskalátoru (drobným zásahem do kódu) | ||
=== Nevýhody === | === Nevýhody === | ||
| − | * ... | + | * Cestující se nemohou předbíhat a ti, kdo na eskalátoru jdou, nemohou přecházet mezi levým a pravým pruhem, což je v praxi běžná věc. |
| + | * Trochu krkolomně se mění frame rate modelu, ale to je dáno omezením NetLoga | ||
| + | * Model uvažuje eskalátory pouze na jedné straně, a to na "dlouhém konci" vestibulu. Některé stanice metra mají více východů a některé z nich jsou třeba uprostřed stanice (Pankrác). | ||
| + | * Neuvažuji zde cestující, kteří se pohybují opačným směrem po protijedoucích eskalátorech nebo ty, kteří ve stanici čekají na metro či nastupují. Pro nastupování a vystupování by bylo zajímavé vytvořit samotnou simulaci, která by však musela značně rozšířit pravidla pro chování agentů (cestujících). | ||
= Výsledky = | = Výsledky = | ||
| + | |||
| + | == Definice problému == | ||
| + | |||
| + | Eskalátory jsou poháněny elektrickou energií a jejich vysoký výkon znamená potřebu vysokého odběru elektrického proudu. Při běhu eskalátoru také dochází k jeho opotřebení, čímž vzniká potřeba pravidelné údržby a čas od času je nutné provést kromě rutinních servisních prací také vyměnit opotřebované či poškozené součásti eskalátoru. | ||
| + | |||
| + | Při hustějším provozu v metru nás (zejména v době konání nějaké akce) na takovýchto eskalátorech v metru nás bude zajímat klíčová otázka : '''Vyplatí se nám zapnout další eskalátor?''' | ||
| + | Abychom si mohli na položenou otázku odpovědět, potřebujeme znát, za jak dlouho cestující průměrně opouští prostor metra. Pro naše potřeby budeme uvažovat, že eskalátory jsou zapnuty již od příjezdu metra do stanice a nevypínají se. Model sleduje jen omezený časový úsek - od příjezdu metra a vyložení cestujících až do opuštění posledního cestujícího vestibul metra (horní část stanice). | ||
| + | |||
| + | Z doby, po kterou jsou cestující v prostorech metra lze snadno vypočítat celkové náklady spojené s provozem eskalátorů, známe-li průměrné náklady za 1 sekundu provozu. Ty se budou značně lišit v závislosti na typu, délce, technického stavu eskalátoru, cenu za služby spojené s údržbou apod. Pro potřeby této simulace budeme zanedbávat potřebu údržby a budeme uvažovat, že 1 kWh stojí 3,71 Kč<ref name="kwh">Cena 1kWh<i>Energie123.cz</i> [online]. [cit. 2016-06-04]. Dostupné z: http://www.energie123.cz/elektrina/ceny-elektricke-energie/cena-1-kwh/</ref> a eskalátor ročně spotřebuje 60 000 kWh<ref name="spotreba">How much energy do escalators use?<i>Slate.com</i> [online]. 2010-08-10 [cit. 2016-06-04]. Dostupné z: http://www.slate.com/articles/health_and_science/the_green_lantern/2010/08/escalators_vs_elevators.html</ref>. Při 20 hodinách denního provozu (uvažujme uzavření metra od 1 do 5 hodin ráno) to činí 60000/(365*20*60*60) = '''0,002283105023''' kWh každou vteřinu, tedy 3,71*0,002283105023 = '''0,008470319635''' Kč za každou vteřinu provozu. V modelu je výchozí hodnota zaokrouhlena na '''0,0085 Kč''' | ||
| + | |||
| + | == Postup řešení problému == | ||
| + | |||
| + | # Nejprve resetujeme simulaci tlačítkem Master Reset na výchozí hodnoty | ||
| + | # Natavíme příjezd 200 cestujících, kteří se budou pohybovat výchozí rychlostí, pevně danou v modelu | ||
| + | # Ve výchozím stavu budeme uvažovat jen aktivní a nejpomalejší (0,5 m/s) eskalátor nejblíže k místu příjezdu. Ostatní eskalátory vypneme | ||
| + | # Fixní náklady budeme považovat za nulové, variabilní náklady ponecháme výchozí, tedy 0,0085 | ||
| + | # Ostatní parametry modelu necháme ve výchozím stavu: | ||
| + | #* Délka eskalátoru 50 m | ||
| + | #* Pravděpodobnost zastavení 0.05 | ||
| + | #* Poměr chodících cestujících 30 % | ||
| + | |||
| + | Nyní simulaci spustíme a zapíšeme si naměřené hodnoty. Protože bude průběh pokaždé trochu jiný, provedeme opakovaný počet pozorování (5) a výsledky zprůměrujeme. | ||
| + | |||
| + | Dále zkusíme změnit nastavení eskalátorů následovně: | ||
| + | * Zvýšíme rychlost jediného aktivního eskalátoru na maximum (0,75 m/s) | ||
| + | * Zapneme navíc eskalátor číslo 3, oběma aktivním eskalátorům nastavíme rychlost 0,5 m/s | ||
| + | * Zapneme všechny eskalátory a nastavíme jim maximální rychlost (0,75 m/s) | ||
| + | |||
| + | == Výsledky == | ||
| + | |||
| + | Z měření jsme dostali hodnoty ze 4 různých scénářů, které jsou znázorněny v následujících obrázcích (tabulkách). Níže jsou zobrazeny i grafy porovnávající čas odchodu a náklady pro jednotlivé scénáře. | ||
| + | |||
| + | <gallery> | ||
| + | File:Xrojr01-s1.png|Obr. 2 Scénář č. 1 | ||
| + | File:Xrojr01-s2.png|Obr. 3 Scénář č. 2 | ||
| + | File:Xrojr01-s3.png|Obr. 4 Scénář č. 3 | ||
| + | File:Xrojr01-s4.png|Obr. 5 Scénář č. 4 | ||
| + | File:Xrojr01-grafy.png|Obr. 6 Srovnání výsledků | ||
| + | </gallery> | ||
| + | |||
| + | Z naměřených hodnot je patrné, že zvýšíme-li počet eskalátorů a jejich rychlost, zkrátíme tím dobu, kterou po kterou musí být zapnuty, protože stihneme přepravit stejný počet cestujících za kratší dobu, což se dalo očekávat. Nás však kromě toho zajímá, který z navrhovaných scénářů bude co nejefektivnější, tedy který dokáže přepravit cestující nejrychleji a zároveň za nejnižší náklady. To můžeme určit pomocí poměru mezi dobou, za kterou odejde polovina cestujících a náklady | ||
= Závěr = | = Závěr = | ||
| − | == Zhodnocení naplnění cíle == | + | Ze získaných poměrů mezi dobou opuštění poloviny cestujících a náklady vidíme, že nejefektivnějším scénářem je scénář č. 4, v němž jsou zapnuty všechny eskalátory na plnou rychlost, protože cestující opustí prostor výrazně rychleji než v případě ostatních scénářů. Výhodnost tohoto scénáře by platila, pokud by v mezičasech mezi příjezdy mohly být eskalátory vypínány. Pokud by vypínány být nemohly, bylo by nejlepší zvolit scénář č. 2, tedy jeden eskalátor s maximální rychlostí. |
| + | |||
| + | Můžeme-li eskalátory vypínat v době, kdy nejsou potřeba se vždy vyplatí další eskalátory zapnout. Pokud však musí být eskalátory v provozu po celou dobu otevření metra, je lepší pouze zvýšit rychlost a další eskalátory zapínat jen v případě nezbytnosti. | ||
| + | |||
| + | == Zhodnocení naplnění cíle práce == | ||
| + | |||
| + | Cílem této práce bylo zjistit optimální nastavení eskalátorů pro dané vstupní parametry, čehož bylo v předchozí kapitole dosaženo. Provedením simulace byla nalezena odpověď na klíčovou otázku '''Vyplatí se nám zapnout další eskalátor?'''. Vytvořený model lze použít pro simulace s různými vstupními parametry a lze jej snadno rozšířit. Cíl práce tedy považuji za naplněný. | ||
| + | |||
| + | == Další možné otázky ke zkoumání == | ||
| + | * Jak se zlepší průměrná rychlost odchodu poloviny cestujících, když budou všichni poslušní, tedy pravděpodobnost jejich zastavení bude rovna 0? | ||
| + | * Jak se na výsledných nákladech projeví větší procento chodících cestujících? | ||
| + | * Jaký vliv má počet cestujících na výsledné náklady? Zkoumejte pro 50, 100, 200 a 300 cestujících. | ||
== Možná rozšíření modelu == | == Možná rozšíření modelu == | ||
| Line 191: | Line 245: | ||
= Zdroje = | = Zdroje = | ||
<references/> | <references/> | ||
| + | |||
| + | = Ke stažení = | ||
| + | |||
| + | [[File:Xrojr01-eskalatory-final.nlogo]] | Vlastní simulace v programu NetLogo 5.3.1 | ||
| + | |||
| + | [[File:Xrojr01-eskalatory-provedeni.xlsx]] | Pomocný XLSX se záznamy z pozorování | ||
Latest revision as of 14:20, 6 June 2016
Contents
Zadání
Název simulace: Optimalizace nastavení eskalátorů v metru
Předmět: 4IT495 Simulace systémů (LS 2015/2016)
Autor: Bc. Robert Rojo
Typ modelu: Multiagentní
Modelovací nástroj: NetLogo 5.3.1
Definice problému
Simulace slouží k nalezení optimální rychlosti a počtu aktivních eskalátorů. Máme situaci s předem danými parametry. Do stanice přijede metro, vyloží cestující a ti jdou k nejbližšímu eskalátoru, přičemž pokud je eskalátorů více, zvolí si jeden z nich, jedoucí danou rychlostí. Někteří cestující jdou, a to po levé straně eskalátoru, někteří stojí na pravé straně. Ti inteligentnější stojí opravdu vpravo tak, aby nevadili těm, kteří chtějí jít. Ti, kterým Pán Bůh tolik nenadělil stojí vlevo, a tak blokují všechny za sebou.
Cíl
Cílem je pomocí vytvořeného modelu minimalizovat počet aktivních eskalátorů, čímž dojde ke snížení nákladů, a minimalizovat dobu, kdy je eskalátor v provozu, což lze odhadnout podle toho, za jakou dobu se všichni dostanou ven z prostoru metra.
Metoda
Pro tuto simulaci jsem zvolil NetLogo, neboť mi šlo o simulování pohybu a interakce mnoha pasažérů v daném známém prostředí - na eskalátorech v metru. Informace o eskalátorech jsem získal z webu Dopravního podniku hlavního města Prahy[1], rychlost eskalátorů a chůze na nich jsem osobně ověřoval měřením ve stanici Háje.
Model
Popis modelu je členěn do několika částí. V úvodu je vysvětleno, jak model pracuje - tento popis jsem převzal z vlastní analýzy problému, kterou jsem provedl před samotnou implementací simulace v nástroji NetLogo. Dále jsou uvedeny agenti, jejich vlastnosti, co je možné v modelu sledovat a jak vypadá uživatelské rozhraní. V závěru jsou uvedeny výhody a nevýhody tohoto modelu.
Jak to celé funguje
Samotnou simulaci je možné rozdělit do tří odlišných fází, kterými každý cestující prochází.
Fáze 1 - Příchod cestujících k eskalátorům.
Zde jde o jednoduché přemístění cestujících k předem určenému bodu.
- Jsou vytvoření cestující u dveří metra. Každý cestující jde svým tempem, které je určeno náhodně při jeho narození.
- Každý cestující si náhodně při svém vzniku vybere, ke kterému eskalátoru půjde (dojde ke "spravedlivému" rozdělení zátěže). V reálu to vypadá velmi podobně, každý se snaží dostat tam, kde je menší fronta, což ve výsledku způsobí rovnoměrné rozložení počtu cestujících u jednotlivých eskalátorů.
- Cestující jde ke svému vybranému eskalátoru, během cesty svou volbu nemění (zde by mohlo být nějaké rozhodování na základě okolních podmínek, což by ale bylo složitější na implementaci)
- Během cesty se snaží cestující vyhnout ostatním, a to tak, že pokud je někdo před ním, otočí se o 45 stupnů do strany a vydá se tím směrem (stále se snaží dojít ke svému eskalátoru).
- Když se cestující dostanou k eskalátoru, dostávají se do fáze 2
Fáze 2 - Stairway to heaven
V této fázi jsou cestující vyvezeni na povrch.
- Cestující si na eskalátoru stoupá vlevo či vpravo, podle své preference, která je určena při jeho narození. Pokud preferuje pravou stranu, pohybuje se ke konci eskalátoru právě rychlostí eskalátoru (na eskalátoru stojí).
- Preferuje-li levou stranu, mohou nastat dvě situace:
- a) pohybuje se rychlostí eskalátoru (také stojí), čímž mimo jiné blokuje ty, kteří chtějí jít (viz b)
- b) pohybuje se vyšší rychlostí než je rychlost eskalátoru (= rychlostí eskalátoru + vlastní rychlostí chůze, danou náhodně při jeho narození)
- V pohybu se cestující chovají podle těchto pravidel:
- preferují-li stání, stojí, dokud nejsou vyvezeni nahoru
- preferují-li chůzi, jdou (po levé straně) kupředu, dokud nenarazí na jiného stojícího cestujícího. V takovém případě se také zastaví.
- Dostanou-li se cestující na konec eskalátoru, dostávají se do fáze 3
Fáze 3 - Opouštění eskalátorů
V této fázi cestující opouští eskalátory a jdou k východu.
- Cestující, kteří opustí eskalátor, pokračují k východu, opět svou rychlostí, která je určena při jejich narození.
- Opět se snaží vyhnout ostatním, pokud jim stojí v cestě, stejně jako před nastoupením na eskalátor.
Agenti a jejich vlastnosti
Hlavními agenty, kteří v simulaci figurují, jsou cestující, eskalátory, východy a zdi.
Cestující (passengers|passenger)
- pace - aktuální rychlost chůze, která se mění v závislosti na tom, zde je cestující na zemi nebo na eskalátoru, viz ground-pace a escalator-pace
- headx - souřadnice x místa, kam cestující míří
- heady - souřadnice x místa, kam cestující míří
- has-exit - true, pokud už má cestující zvolen východ, kterým vyjde po opuštění eskalátoru
- preference - "stand" nebo "walk". Určuje, zda cestující bude na eskalátoru stát (bude modrý) či chodit (bude žlutý)
- escalator-pace - Rychlost chůze na eskalátoru (0,4-1,0 m/s) - V modelu pevně nastaveno jako polovina, tedy 0,2-0.5 z důvodu přepočítávání pro potřeby měření času. Pro situaci jsem zvolil rovnoměrné rozdělení, i když správnější by bylo využít normální či lognormální rozdělení (u kterých je však problém určit parametry tak, aby se nerodili cestující, kteří chodí pozpátku)
- ground-pace - Rychlost chůze na zemi (1-1,5 m/s). V modelu pevně nastaveno jako polovina , tedy 0,5-0.75 z důvodu přepočítávání pro potřeby měření času. Pro situaci jsem zvolil rovnoměrné rozdělení, i když správnější by bylo využít normální či lognormální rozdělení (u kterých je však problém určit parametry tak, aby se nerodili cestující, kteří chodí pozpátku)
- escalator-id - Jednoznačný identifikátor eskalátoru, ke kterému cestující jde a po kterém je vyvezen.
- ready-to-ride - Slouží pro potřeby "vstupu" na eskalátor, kdy je potřeba, aby se část kódu provedla pouze jednou.
- previous-x - Předchozí pozice x cestujícího. Slouží k určování, zda stojí cestující moc dlouho na jednom místě a je někde zaseknutý.
- previous-y - Předchozí pozice y cestujícího. Slouží k určování, zda stojí cestující moc dlouho na jednom místě a je někde zaseknutý.
- ticks-standing - Počet tiknutí, které stojí cestující na stejném místě. Slouží k určování, zda stojí cestující moc dlouho na jednom místě a je někde zaseknutý.
- is-clogging - Vlastnost, která je cestujícímu přidělena na základě pravděpodobnosti blokování p-of-clogging. Blokující cestující je označen červeně.
Eskalátory (escalators|escalator)
- id - jednoznačný identifikátor eskalátoru. Jedná se spíše o pomocnou proměnnou při určování rychlosti cestujícího na eskalátoru. Ten totiž musí vědět, na kterém eskalátoru je (viz escalator-id u cestujícího).
- speed - Rychlost samotného eskalátoru (0,5-0,75 m/s). Interval rychlosti je dán směrnicí EU.
- padx - Pozice x eskalátoru. Eskalátory mají pevně danou šířku, která při přepoču neodpovídá skutečnosti, ale pro potřeby modelu to nijak nevadí.
- pady - Pozice y eskalátoru
- is-active - Je-li "true", mohou si cestující tento eskalátor vybrat, jít k němu a nechat se vyvézt nahoru. Také slouží k určení výpočtu nákladů - ty se počítají pouze z aktivních eskalátorů. Aktivní eskalátory jsou označeny zelenou barvou, neaktivní pak barvou červenou.
Dveře - východy (doors|door)
Počet, velikost i pozice dveří je pevně daná, neboť se model zaměřuje primárně na pohyb na eskalátorech
- doorx - Souřadnice x dveří.
- doory - Souřadnice x dveří.
Zdi (walls|wall)
Zdi jsou v modelu proto, aby nemohli cestující obejít nástupní plochu eskalátoru a nastoupit třeba až v polovině eskalátoru. Zdi jsou v modelu viditelné jako světle hnědá plocha v pásmu s eskalátory.
- posx - Souřadnice x 1 bloku zdi.
- posy - Souřadnice x 1 bloku zdi.
Vstupní parametry a nastavení modelu
Nastavení cestujících (pasažérů)
- passengers-count - Počet cestujících (z Poissonova rozdělení nebo přesně - přepíná se volbou is-poisson)
- is-poisson - Je-li volba aktivní, je počet pasažárů parametrem Poissonova rozdělení, jinak je vytvořen jejich přesný počet.
- walkers-ratio - Poměr stojících a chodících cestujících z intervalu <0;1>, 0 znaměná pouze stojící cestující, 1 pouze chodící
- p-of-clogging - Pravděpodobnost, že narozený chodící cestující bude na eskalátoru stát. Lze nastavit v intervalu <0;0,3> (0,3 je poměrně veliké množství, proto volím jemnější krokování 0,01 a shora omezený interval pravděpodobnosti)
- keep-distance - Aktivní volba zapíná kolize mezi chodícími na eskalátoru (když se před cestujícím někdo zastaví, musí se taky zastavit)
- unstuck-timeout - Pokud je pasažér tento počet tiknutí pořád na stejném místě, je zaseklý, a musí udělat krok zpět o náhodnou vzdálenost <0;0.5>. tím je zaručeno, že se ve velké mačkanici cestující nezaseknou a vždy mohou pokračovat ve své cestě.
Nastavení eskalátorů
- escalator-length - Délka eskalátorů v metrech, lze nastavit posuvníkem v intervalu <0;100>
- escalator-n - Počet aktivních eskalátorů, nastavuje se zvlášť pro každý eskalátor (escalator-1, escalator-2, escalator-3, escalator-4)
- escalator-n-speed - Rychlost každého z eskalátorů (escalator-1-speed, escalator-2-speed, escalator-3-speed, escalator-4-speed)
Další nastavení
- debug - Aktivní volba zapíná ladící mód, kdy je vytvořen jen jeden cestující blízko eskalátorů. To je užitečné při zkoumání jeho rychlosti a pozice na eskalátoru.
- frame-rate - Aby správně fungoval přepočet měřáků na sekundy, musí být tato hodnota nastavena stejně jako hodnota "frame rate" v nastavení modelu a model musí být v "normal speed" rychlosti. Hodnota v nastavení modelu musí být nastavena bohužel zvlášť ručně.
Nastavení nákladů
- fixed-costs-per-escalator - Fixní náklady pro každý aktivní eskalátor. (Můžeme situaci ještě před vybudováním eskalátorů, kdy nás zajímají např. pořizovací náklady)
- variable-costs-per-second - Náklady na každý aktivní eskalátor za každou vteřinu provozu.
Ovládání
Ovládat simulaci lze následujícími tlačítky, které jsou v sekci Ovládání:
- Setup - Připraví model k použití s aktuálně nastavenými parametry
- Go - Spustí simulaci. Opětovným stiskem lze simulaci zastavit. Mějte však na paměti, že pozastavením simulace nebude zastaven měřený čas.
- Step - Při krokování opět dojde k "rozbití" měření času. To je dáno tím, že čas se odvíjí od běhu času ve virtuálním prostředí Javy. Krokování je spíše vhodné pro potřeby ladění.
- Master Reset - Nastaví všechny hodnoty na výchozí a provede Setup.
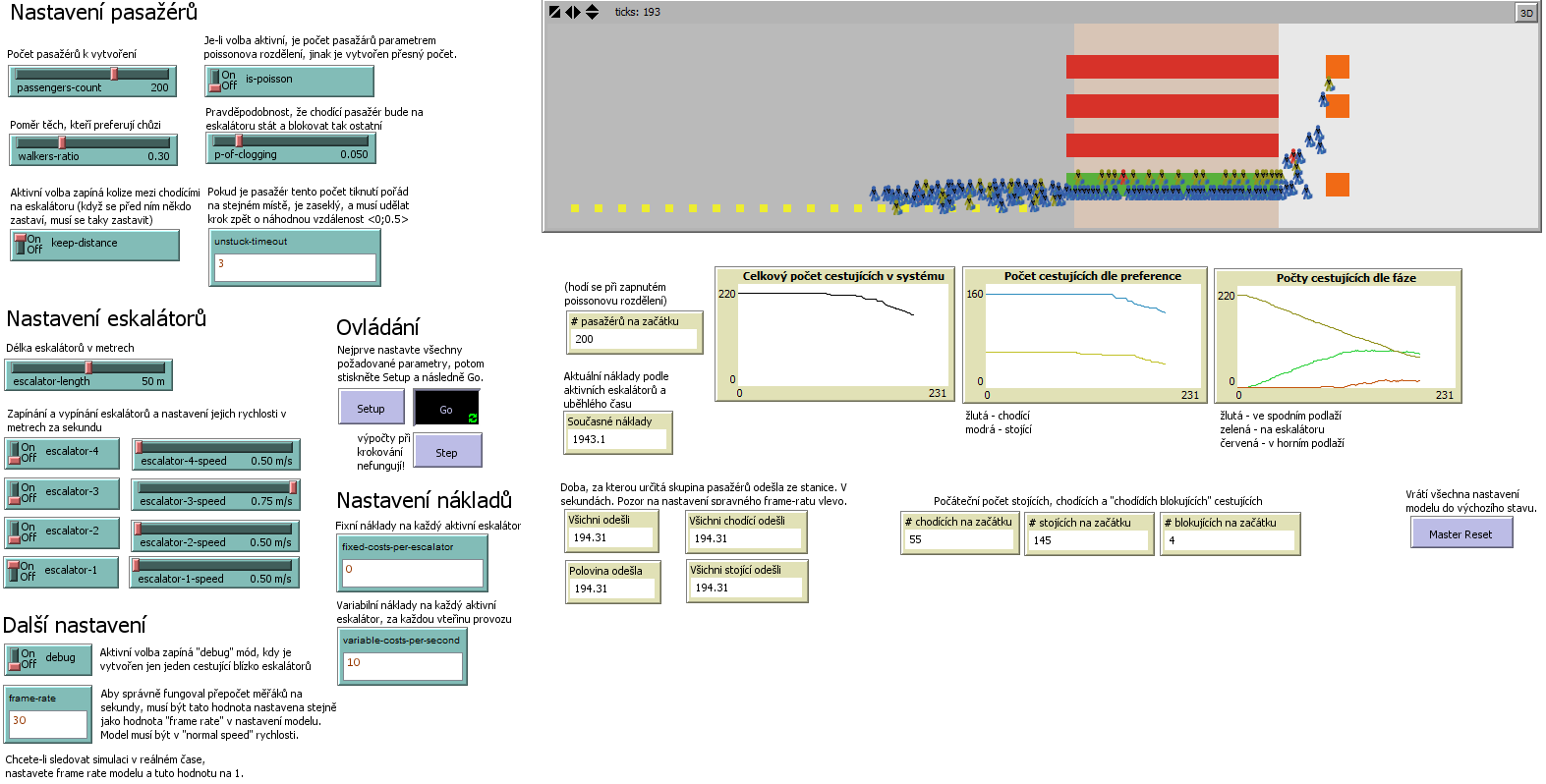
Sledované ukazatelé
Číselné ukazatelé
- total-passengers - (# pasažérů na začátku) - Zobrazuje, kolik cestujících (pasažérů) je na začátku vytvořeno. Informace se hodí v případě zapnuté volby is-poisson, kdy není počet cestujících přímo zadaný.
- actual-costs - (Současné náklady) - Zobrazuje aktuálně vypočtené náklady podle aktivních eskalátorů a uběhlého času.
- time - (Všichni odešli) - Čas, za který všichni cestující opustili systém (metro).
- half-time - (Polovina odešla) - Čas, za který metro opustila polovina všech původních cestujících.
- walking-time - (Všichni chodící odešli) - Čas, za který všichni eskalátorech chodící cestující.
- standing-time - (Všichni stojící odešli) - Čas, za který z metra odešlo všichni na eskalátorech stojící cestující opustili.
Grafy
- Celkový počet cestujících v systému - Zobrazuje vývoj počtu cestujících v metru. na začátku jsou zde všichni a s postupem času křivka klesá, jak cestující vychází ven z prostorů metra.
- Počet cestujících dle preference - Zobrazuje to samé jako předchozí graf, jen zvlášť pro chodící (žlutá křivka) a stojící (modrá křivka).
- Počty cestujících dle fáze - Zobrazuje vývoj počtu cestujících v jednotlivých fázích
- Fáze 1 - spodní podlaží (žlutá)
- Fáze 2 - eskalátory (zelená)
- Fáze 3 - horní podlaží (červená)
Pozn.: Je-li nastaven frame-rate na 30, zobrazuje osa x v grafech čas ve vteřinách
Grafické rozhraní
Níže je zobrazeno, jak vypadá rozhraní simulace.
Výhody a nevýhody modelu
Aby byl cíl semestrální práce naplněn v daném čase a s mými danými znalostmi a zkušenostmi, nebylo možné implementovat všechny nápady s touto problematikou spojené. Z povahy a konkrétní implementace modelu vyplývají výhody i nevýhody, které jsou shrnuty níže.
Výhody
- Model ukazuje výsledky v reálném čase nebo zrychleně, přičemž vždy zobrazuje skutečné hodnoty v sekundách.
- Je pokryt nejčastější stav na eskalátorech, a to včetně zastavení někoho v pohybující se řadě.
- Model umí kromě časů opuštění počítat i s náklady, což zvyšuje komfort uživateli.
- Model lze snadno rozšířit o nové zajímavé funkcionality
- V modelu lze snadno vyměnit rozdělení, ze kterých jsou generovány vlastnosti cestujících a eskalátoru (drobným zásahem do kódu)
Nevýhody
- Cestující se nemohou předbíhat a ti, kdo na eskalátoru jdou, nemohou přecházet mezi levým a pravým pruhem, což je v praxi běžná věc.
- Trochu krkolomně se mění frame rate modelu, ale to je dáno omezením NetLoga
- Model uvažuje eskalátory pouze na jedné straně, a to na "dlouhém konci" vestibulu. Některé stanice metra mají více východů a některé z nich jsou třeba uprostřed stanice (Pankrác).
- Neuvažuji zde cestující, kteří se pohybují opačným směrem po protijedoucích eskalátorech nebo ty, kteří ve stanici čekají na metro či nastupují. Pro nastupování a vystupování by bylo zajímavé vytvořit samotnou simulaci, která by však musela značně rozšířit pravidla pro chování agentů (cestujících).
Výsledky
Definice problému
Eskalátory jsou poháněny elektrickou energií a jejich vysoký výkon znamená potřebu vysokého odběru elektrického proudu. Při běhu eskalátoru také dochází k jeho opotřebení, čímž vzniká potřeba pravidelné údržby a čas od času je nutné provést kromě rutinních servisních prací také vyměnit opotřebované či poškozené součásti eskalátoru.
Při hustějším provozu v metru nás (zejména v době konání nějaké akce) na takovýchto eskalátorech v metru nás bude zajímat klíčová otázka : Vyplatí se nám zapnout další eskalátor? Abychom si mohli na položenou otázku odpovědět, potřebujeme znát, za jak dlouho cestující průměrně opouští prostor metra. Pro naše potřeby budeme uvažovat, že eskalátory jsou zapnuty již od příjezdu metra do stanice a nevypínají se. Model sleduje jen omezený časový úsek - od příjezdu metra a vyložení cestujících až do opuštění posledního cestujícího vestibul metra (horní část stanice).
Z doby, po kterou jsou cestující v prostorech metra lze snadno vypočítat celkové náklady spojené s provozem eskalátorů, známe-li průměrné náklady za 1 sekundu provozu. Ty se budou značně lišit v závislosti na typu, délce, technického stavu eskalátoru, cenu za služby spojené s údržbou apod. Pro potřeby této simulace budeme zanedbávat potřebu údržby a budeme uvažovat, že 1 kWh stojí 3,71 Kč[2] a eskalátor ročně spotřebuje 60 000 kWh[3]. Při 20 hodinách denního provozu (uvažujme uzavření metra od 1 do 5 hodin ráno) to činí 60000/(365*20*60*60) = 0,002283105023 kWh každou vteřinu, tedy 3,71*0,002283105023 = 0,008470319635 Kč za každou vteřinu provozu. V modelu je výchozí hodnota zaokrouhlena na 0,0085 Kč
Postup řešení problému
- Nejprve resetujeme simulaci tlačítkem Master Reset na výchozí hodnoty
- Natavíme příjezd 200 cestujících, kteří se budou pohybovat výchozí rychlostí, pevně danou v modelu
- Ve výchozím stavu budeme uvažovat jen aktivní a nejpomalejší (0,5 m/s) eskalátor nejblíže k místu příjezdu. Ostatní eskalátory vypneme
- Fixní náklady budeme považovat za nulové, variabilní náklady ponecháme výchozí, tedy 0,0085
- Ostatní parametry modelu necháme ve výchozím stavu:
- Délka eskalátoru 50 m
- Pravděpodobnost zastavení 0.05
- Poměr chodících cestujících 30 %
Nyní simulaci spustíme a zapíšeme si naměřené hodnoty. Protože bude průběh pokaždé trochu jiný, provedeme opakovaný počet pozorování (5) a výsledky zprůměrujeme.
Dále zkusíme změnit nastavení eskalátorů následovně:
- Zvýšíme rychlost jediného aktivního eskalátoru na maximum (0,75 m/s)
- Zapneme navíc eskalátor číslo 3, oběma aktivním eskalátorům nastavíme rychlost 0,5 m/s
- Zapneme všechny eskalátory a nastavíme jim maximální rychlost (0,75 m/s)
Výsledky
Z měření jsme dostali hodnoty ze 4 různých scénářů, které jsou znázorněny v následujících obrázcích (tabulkách). Níže jsou zobrazeny i grafy porovnávající čas odchodu a náklady pro jednotlivé scénáře.
Z naměřených hodnot je patrné, že zvýšíme-li počet eskalátorů a jejich rychlost, zkrátíme tím dobu, kterou po kterou musí být zapnuty, protože stihneme přepravit stejný počet cestujících za kratší dobu, což se dalo očekávat. Nás však kromě toho zajímá, který z navrhovaných scénářů bude co nejefektivnější, tedy který dokáže přepravit cestující nejrychleji a zároveň za nejnižší náklady. To můžeme určit pomocí poměru mezi dobou, za kterou odejde polovina cestujících a náklady
Závěr
Ze získaných poměrů mezi dobou opuštění poloviny cestujících a náklady vidíme, že nejefektivnějším scénářem je scénář č. 4, v němž jsou zapnuty všechny eskalátory na plnou rychlost, protože cestující opustí prostor výrazně rychleji než v případě ostatních scénářů. Výhodnost tohoto scénáře by platila, pokud by v mezičasech mezi příjezdy mohly být eskalátory vypínány. Pokud by vypínány být nemohly, bylo by nejlepší zvolit scénář č. 2, tedy jeden eskalátor s maximální rychlostí.
Můžeme-li eskalátory vypínat v době, kdy nejsou potřeba se vždy vyplatí další eskalátory zapnout. Pokud však musí být eskalátory v provozu po celou dobu otevření metra, je lepší pouze zvýšit rychlost a další eskalátory zapínat jen v případě nezbytnosti.
Zhodnocení naplnění cíle práce
Cílem této práce bylo zjistit optimální nastavení eskalátorů pro dané vstupní parametry, čehož bylo v předchozí kapitole dosaženo. Provedením simulace byla nalezena odpověď na klíčovou otázku Vyplatí se nám zapnout další eskalátor?. Vytvořený model lze použít pro simulace s různými vstupními parametry a lze jej snadno rozšířit. Cíl práce tedy považuji za naplněný.
Další možné otázky ke zkoumání
- Jak se zlepší průměrná rychlost odchodu poloviny cestujících, když budou všichni poslušní, tedy pravděpodobnost jejich zastavení bude rovna 0?
- Jak se na výsledných nákladech projeví větší procento chodících cestujících?
- Jaký vliv má počet cestujících na výsledné náklady? Zkoumejte pro 50, 100, 200 a 300 cestujících.
Možná rozšíření modelu
Současný model zachycuje základní principy a bylo by jej možné a vhodné rozšířit v několika aspektech, např.:
- Předbíhání na eskalátorech - Hlavním nedostatkem modelu je úvaha, že ti, kdo stojí vpravo nikdy nejdou. V praxi se obvykle cestující podle potřeby umí vyhýbat, a tedy přeskakovat z levého do pravého pruhu a zpět podle potřeby.
- Automatizace několika běhů - Pro pohodlí uživatele a předcházení manuálním chybám při zkoumání výsledků by mohl model v předen nastavených časových intervalech generovat další cestující o daném počtu. Bylo by tam možné zkoumat, zda nejsou intervaly příjezdu metra natolik krátké, že původní cestující nestihnout odejít před příjezdem dalších.
- Možnost říct "s dovolením" - Cestující za někým stojícím by ho mohl požádat o uvolnění místa a ten by mu mohl vyhovět či ne.
- Více východů/přestupy - Např. ve stanici Můstek na linkách A a B se lze shledat s poměrně komplexním systémem východů a více eskalátory.
- Rozšíření o běžné schodiště - Případ stanice Muzeum, kde nalezneme dva eskalátory (jeden nahoru, jeden dolů) a běžné schodiště.
- Přidání lidí v opačném směru - Zajímavé by bylo sledovat pohyb cestujících při různém nastavení eskalátorů (např. 3 jedou nahoru, jeden dolů) a vzájemnou interakci cestujících blízko u nástupu a výstupu z eskalátorů. V praxi vidím, že se často lidé neumí vyhnout.
- Přidání třetí dimenze - Zde by šlo spíše o lepší vizuální přehlednost.
Zdroje
- ↑ Dopravní podnik vymění ve stanicích metra eskalátory za 100 milionů korun Dopravní podnik hlavního města Prahy [online]. 2013-04-24 [cit. 2016-05-20]. Dostupné z: http://www.dpp.cz/dopravni-podnik-vymeni-ve-stanicich-metra-eskalatory-za-100-milionu-korun/
- ↑ Cena 1kWhEnergie123.cz [online]. [cit. 2016-06-04]. Dostupné z: http://www.energie123.cz/elektrina/ceny-elektricke-energie/cena-1-kwh/
- ↑ How much energy do escalators use?Slate.com [online]. 2010-08-10 [cit. 2016-06-04]. Dostupné z: http://www.slate.com/articles/health_and_science/the_green_lantern/2010/08/escalators_vs_elevators.html
Ke stažení
File:Xrojr01-eskalatory-final.nlogo | Vlastní simulace v programu NetLogo 5.3.1
File:Xrojr01-eskalatory-provedeni.xlsx | Pomocný XLSX se záznamy z pozorování